Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Jun 20;20(Suppl 12):321.
doi: 10.1186/s12859-019-2832-3.

Optimal clustering with missing values

Shahin Boluki  1 , Siamak Zamani Dadaneh  1 , Xiaoning Qian  1   2 , Edward R Dougherty  3   4
Affiliations

Optimal clustering with missing values

Shahin Boluki et al. BMC Bioinformatics. .

Abstract

Background: Missing values frequently arise in modern biomedical studies due to various reasons, including missing tests or complex profiling technologies for different omics measurements. Missing values can complicate the application of clustering algorithms, whose goals are to group points based on some similarity criterion. A common practice for dealing with missing values in the context of clustering is to first impute the missing values, and then apply the clustering algorithm on the completed data.

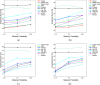
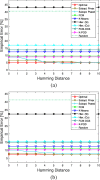
Results: We consider missing values in the context of optimal clustering, which finds an optimal clustering operator with reference to an underlying random labeled point process (RLPP). We show how the missing-value problem fits neatly into the overall framework of optimal clustering by incorporating the missing value mechanism into the random labeled point process and then marginalizing out the missing-value process. In particular, we demonstrate the proposed framework for the Gaussian model with arbitrary covariance structures. Comprehensive experimental studies on both synthetic and real-world RNA-seq data show the superior performance of the proposed optimal clustering with missing values when compared to various clustering approaches.

Conclusion: Optimal clustering with missing values obviates the need for imputation-based pre-processing of the data, while at the same time possessing smaller clustering errors.

Keywords: Clustering; Missing data; Optimal design; Pattern recognition.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no competing interests.

Figures

Fig. 1
Fig. 1
Average clustering errors vs. missing probability for fixed means and covariances model. The first and second rows correspond to n=20 and n=70, respectively. a n1=10,n2=10, b n1=12,n2=8, c n1=35,n2=35, d n1=42,n2=28
Fig. 2
Fig. 2
Average clustering errors vs. missing probability for Gaussian means and fixed covariances model. The first and second rows correspond to n=20 and n=70, respectively. a n1=10,n2=10, b n1=12,n2=8, c n1=35,n2=35, d n1=42,n2=28
Fig. 3
Fig. 3
Average clustering errors for Gaussian means and inverse-Wishart covariances model. The first row corresponds to n=20, and the errors are shown for different missing probabilities. The second row corresponds to n=70 and missing probability of 0.15, where the errors are plotted vs. the Hamming distance threshold used to define the reference partitions in Pseed. a n1=10,n2=10, b n1=12,n2=8, c n1=35,n2=35,miss. prob.=0.15, d n1=42,n2=28,miss. prob.=0.15
Fig. 4
Fig. 4
Empirical clustering errors on breast cancer RNA-seq data. a n1=10,n2=10,miss. prob.=0.15, b n1=12,n2=8,miss. prob.=0.15
See this image and copyright information in PMC

References

    1. Ben-Dor A, Shamir R, Yakhini Z. Clustering gene expression patterns. J Comput Biol. 1999;6:281–97. - PubMed
    1. Bittner M, Meitzer P, Chen Y, Jiang Y, Seftor E, Hendrix M, Radmacher M, Simon R, Yakhini Z, Ben-Dor A, Sampas N, Dougherty E, Wang E, Marincola F, Gooden C, Lueders J, Glatfelter A, Pollock P, Carpten J, Gillanders E, Leja D, Dietrich K, Beaudry C, Berens M, Alberts D, Sondak V, Hayward N, Trent J. Molecular classification of cutaneous malignant melanoma by gene expression profiling. J Comput Biol. 2000;406(3):536–40. - PubMed
    1. Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17(10):977–87. - PubMed
    1. Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc. 2002;97(458):611–31.
    1. MacEachern SN, Müller P. Estimating mixture of Dirichlet process models. J Comput Graph Stat. 1998;7(2):223–38.

LinkOut - more resources