Comment on 'Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size'
- PMID: 31219782
- PMCID: PMC6586461
- DOI: 10.7554/eLife.44718
Comment on 'Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size'
Abstract
A recent molecular dynamics investigation into the stability of hemoglobin concluded that the unliganded protein is only stable in the T state when a solvent box is used in the simulations that is ten times larger than what is usually employed (El Hage et al., 2018). Here, we express three main concerns about that study. In addition, we find that with an order of magnitude more statistics, the reported box size dependence is not reproducible. Overall, no significant effects on the kinetics or thermodynamics of conformational transitions were observed.
Keywords: box size; hemoglobin; human; kinetics; molecular biophysics; molecular dynamics; structural biology; thermodynamics.
© 2019, Gapsys and de Groot.
Conflict of interest statement
VG, Bd No competing interests declared
Figures

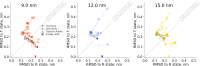

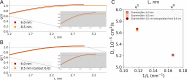
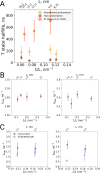

Comment in
-
Response to comment on 'Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size'.Elife. 2019 Jun 20;8:e45318. doi: 10.7554/eLife.45318. Elife. 2019. PMID: 31219783 Free PMC article.
Comment on
-
Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size.Elife. 2018 Jul 12;7:e35560. doi: 10.7554/eLife.35560. Elife. 2018. PMID: 29998846 Free PMC article.
Similar articles
-
On the importance of statistics in molecular simulations for thermodynamics, kinetics and simulation box size.Elife. 2020 Aug 19;9:e57589. doi: 10.7554/eLife.57589. Elife. 2020. PMID: 32812868 Free PMC article.
-
Response to comment on 'Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size'.Elife. 2019 Jun 20;8:e45318. doi: 10.7554/eLife.45318. Elife. 2019. PMID: 31219783 Free PMC article.
-
Valid molecular dynamics simulations of human hemoglobin require a surprisingly large box size.Elife. 2018 Jul 12;7:e35560. doi: 10.7554/eLife.35560. Elife. 2018. PMID: 29998846 Free PMC article.
-
Advances in implicit models of water solvent to compute conformational free energy and molecular dynamics of proteins at constant pH.Adv Protein Chem Struct Biol. 2011;85:281-322. doi: 10.1016/B978-0-12-386485-7.00008-9. Adv Protein Chem Struct Biol. 2011. PMID: 21920327 Review.
-
Coupled binding-bending-folding: The complex conformational dynamics of protein-DNA binding studied by atomistic molecular dynamics simulations.Biochim Biophys Acta. 2015 May;1850(5):1091-1098. doi: 10.1016/j.bbagen.2014.08.009. Epub 2014 Aug 23. Biochim Biophys Acta. 2015. PMID: 25161164 Review.
Cited by
-
Pore mutation N617D in the skeletal muscle DHPR blocks Ca2+ influx due to atypical high-affinity Ca2+ binding.Elife. 2021 Jun 1;10:e63435. doi: 10.7554/eLife.63435. Elife. 2021. PMID: 34061024 Free PMC article.
-
On the importance of statistics in molecular simulations for thermodynamics, kinetics and simulation box size.Elife. 2020 Aug 19;9:e57589. doi: 10.7554/eLife.57589. Elife. 2020. PMID: 32812868 Free PMC article.
-
A single mutation in dairy cow-associated H5N1 viruses increases receptor binding breadth.Nat Commun. 2024 Dec 30;15(1):10768. doi: 10.1038/s41467-024-54934-3. Nat Commun. 2024. PMID: 39737954 Free PMC article.
-
Biomolecular Modeling and Simulation: A Prospering Multidisciplinary Field.Annu Rev Biophys. 2021 May 6;50:267-301. doi: 10.1146/annurev-biophys-091720-102019. Epub 2021 Feb 19. Annu Rev Biophys. 2021. PMID: 33606945 Free PMC article.
-
Shark Antibody Variable Domains Rigidify Upon Affinity Maturation-Understanding the Potential of Shark Immunoglobulins as Therapeutics.Front Mol Biosci. 2021 Apr 20;8:639166. doi: 10.3389/fmolb.2021.639166. eCollection 2021. Front Mol Biosci. 2021. PMID: 33959632 Free PMC article.
References
-
- Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1-2:19–25. doi: 10.1016/j.softx.2015.06.001. - DOI
-
- Darden T, York D, Pedersen L. Particle mesh Ewald: An N ⋅log( N ) method for Ewald sums in large systems. Journal of Chemical Physics. 1993;98:10089–10092. doi: 10.1063/1.464397. - DOI
-
- Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. Journal of Chemical Physics. 1995;103:8577–8593. doi: 10.1063/1.470117. - DOI
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

