The Lyapunov spectra of quantum thermalisation

Abstract

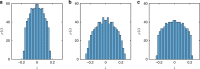
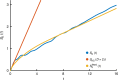
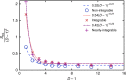
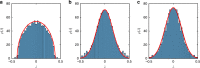
Thermalisation in closed quantum systems occurs through a process of dephasing due to parts of the system outside of the window of observation, gradually revealing the underlying thermal nature of eigenstates. In contrast, closed classical systems thermalize due to dynamical chaos. We demonstrate a deep link between these processes. Projecting quantum dynamics onto variational states using the time-dependent variational principle, results in classical chaotic Hamiltonian dynamics. We study an infinite spin chain in two ways-using the matrix product state ansatz for the wavefunction and for the thermofield purification of the density matrix-and extract the full Lyapunov spectrum of the resulting dynamics. We show that the entanglement growth rate is related to the Kolmogorov-Sinai entropy of dynamics projected onto states with appropriate entanglement, extending previous results about initial entanglement growth to all times. The Lyapunov spectra for thermofield descriptions of thermalizing systems show a remarkable semi-circular distribution.

Fig. 1

Lyapunov spectrum for a wavefunction MPS representation of Ising model dynamics. a Non-integrable case with J = 1, h^x = 0.5, h^x = 1. b Integrable case with J = 1, h^x = 0.5, h^x = 0. c Nearly Integrable case with J = 1, h^x = 0.5, h^x = 0.1. In all cases, the spectrum is obtained for an MPS representation of the wavefunction at bond order D = 20

Fig. 2

Maximum Lyapunov exponent versus bond order. The maximum Lyapunov exponent depends strongly upon the projection nonlinearities at different bond orders, tending to zero in the limit D → ∞. Here, we show the largest exponent varying with bond order for non-integrable (circles), integrable (crosses) and nearly integrable (pluses) systems. The largest exponent decreases like λ_max(D) = 0.32(D − 1)^−0.21 for non-integrable systems, λ_max(D) = 0.54(D − 1)^−0.27 for integrable systems and λ_max(D) = 0.42(D − 1)^−0.22 for nearly integrable systems

Fig. 3

Maximum Lyapunov exponent versus energy density. It has previously been conjectured that λ_max ≤ 2πk_BT/ħ, here, we observe that λ_max (D = 2) increases with energy density above the ground state, but appears to saturated at E ≈ 0.6. The initial growth of λ_max was fitted with a power law 1.80E^1.69

Fig. 4

Entanglement entropy across a bond compared to randomly distributed Schmidt coefficients. At a given bond dimension, the entanglement entropy will saturate after a short time. The saturation value for the entanglement entropy is in strong agreement with a random uniform distribution of Schmidt coefficients

Fig. 5

Entanglement entropy and Kolmogorov–Sinai entropy. The gradient of the entanglement entropy is determined by the Kolmogorov–Sinai entropy. The Kolmogorov–Sinai entropy at D = 2 accurately predicts the gradient of the entanglement entropy at t = 0 (orange). Substituting fitted forms for the Lyapunov spectrum and saturation entanglement into Eq. (4) gives a zero-parameter fit to the entanglement entropy (yellow). This fits may both be compared with the time evolution of S_E(t) found using iTEBD at D = 100

Fig. 6

Kolmogorov–Sinai entropy versus bond order. The Kolmogorov–Sinai entropy scaled by (D − 1)² is related to entanglement growth at short times. Here, we show the scaled KS entropy varying with bond order for non-integrable (circles), integrable (crosses) and nearly integrable (pluses) systems. The non-integrable KS entropy decreases like 0.14 + 1.6e^{−1.08(D−1)}, the Integrable KS entropy decreases like 0.19 + 6.6e^{−1.32(D−1)} and the nearly integrable KS entropy decreases like 0.19 + 11.4e^{−1.81(D−1)}

Fig. 7

Lyapunov Spectrum for a thermofield MPS respresentation of Ising model dynamics. a Non-integrable case with J = 1, h^x = 0.5, h^z = 1. b Integrable case with J = 1, h^x = 0.5, h^z = 0. c Nearly integrable case with J = 1, h^x = 0.5, h^z = 0.1. In all cases, the spectrum is obtained for a wavefunction MPS at bond order $\mathbb{D}=16$. The non-integrable case appears to fit a semi-circle distribution with radius r = 0.39, the integrable case appears to be Gaussian with standard deviation σ = 0.167 and the nearly integrable case appears to be Gaussian with standard deviation σ = 0.161

Fig. 8

Maximum Lyapunov exponent vs. thermofield MPS bond order for the non-integrable system. The largest Lyapunov exponent for the Ising model with J = 1, h^x = 0.5, h^z = 1.0 obtained for an MPS representation of the thermofield double. The exponent appears to be approaching zero like ${\lambda }_{\max }=1.09{\mathbb{D}}^{-0.373}$

Fig. 9

Kolmogorov–Sinai entropy vs. thermofield MPS bond order for non-integrable system. The Kolmogorov–Sinai entropy for the Ising model with J = 1, h^x = 0.5, h^z = 1.0 obtained for an MPS representation of the thermofield double. The KS entropy appears to be divering, growing like $S_{\mathrm{KS}}=1.4270{\mathbb{D}}^{1.58}$