A model for epidemic dynamics in a community with visitor subpopulation
- PMID: 31228488
- PMCID: PMC7094103
- DOI: 10.1016/j.jtbi.2019.06.020
A model for epidemic dynamics in a community with visitor subpopulation
Abstract
With a five dimensional system of ordinary differential equations based on the SIR and SIS models, we consider the dynamics of epidemics in a community which consists of residents and short-stay visitors. Taking different viewpoints to consider public health policies to control the disease, we derive different basic reproduction numbers and clarify their common/different mathematical natures so as to understand their meanings in the dynamics of the epidemic. From our analyses, the short-stay visitor subpopulation could become significant in determining the fate of diseases in the community. Furthermore, our arguments demonstrate that it is necessary to choose one variant of basic reproduction number in order to formulate appropriate public health policies.
Keywords: Basic reproduction number; Epidemic dynamics; Mathematical model; Ordinary differential equations; Public health.
Copyright © 2019 Elsevier Ltd. All rights reserved.
Figures





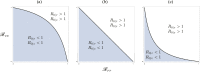


References
-
- Arino J., van den Driessche P. Disease spread in metapopulations. Fields Inst. Commun. 2006;48:1–13.
-
- Ball F., Britton T., House T., Isham V., Mollison D., Pellis L., Scalia Tomba G. Seven challenges for metapopulation models of epidemics, including households models. Epidemics. 2015;10:63–67. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

