The logic behind neural control of breathing pattern
- PMID: 31235701
- PMCID: PMC6591426
- DOI: 10.1038/s41598-019-45011-7
The logic behind neural control of breathing pattern
Abstract
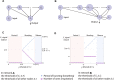
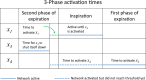
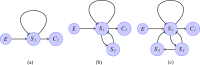
The respiratory rhythm generator is spectacular in its ability to support a wide range of activities and adapt to changing environmental conditions, yet its operating mechanisms remain elusive. We show how selective control of inspiration and expiration times can be achieved in a new representation of the neural system (called a Boolean network). The new framework enables us to predict the behavior of neural networks based on properties of neurons, not their values. Hence, it reveals the logic behind the neural mechanisms that control the breathing pattern. Our network mimics many features seen in the respiratory network such as the transition from a 3-phase to 2-phase to 1-phase rhythm, providing novel insights and new testable predictions.
Conflict of interest statement
The authors declare no competing interests.
Figures





Similar articles
-
Effects of ion channel noise on neural circuits: an application to the respiratory pattern generator to investigate breathing variability.J Neurophysiol. 2017 Jan 1;117(1):230-242. doi: 10.1152/jn.00416.2016. Epub 2016 Oct 19. J Neurophysiol. 2017. PMID: 27760817 Free PMC article.
-
Widespread depolarization during expiration: a source of respiratory drive?Med Hypotheses. 2015 Jan;84(1):31-7. doi: 10.1016/j.mehy.2014.11.010. Epub 2014 Nov 18. Med Hypotheses. 2015. PMID: 25434482
-
A closed-loop model of the respiratory system: focus on hypercapnia and active expiration.PLoS One. 2014 Oct 10;9(10):e109894. doi: 10.1371/journal.pone.0109894. eCollection 2014. PLoS One. 2014. PMID: 25302708 Free PMC article.
-
Understanding the rhythm of breathing: so near, yet so far.Annu Rev Physiol. 2013;75:423-52. doi: 10.1146/annurev-physiol-040510-130049. Epub 2012 Oct 29. Annu Rev Physiol. 2013. PMID: 23121137 Free PMC article. Review.
-
Brainstem respiratory networks: building blocks and microcircuits.Trends Neurosci. 2013 Mar;36(3):152-62. doi: 10.1016/j.tins.2012.11.004. Epub 2012 Dec 17. Trends Neurosci. 2013. PMID: 23254296 Free PMC article. Review.
Cited by
-
Relationship between cardiorespiratory phase coherence during hypoxia and genetic polymorphism in humans.J Physiol. 2020 May;598(10):2001-2019. doi: 10.1113/JP278829. Epub 2020 Feb 26. J Physiol. 2020. PMID: 31957891 Free PMC article.
-
Dynamical consequences of sensory feedback in a half-center oscillator coupled to a simple motor system.Biol Cybern. 2021 Apr;115(2):135-160. doi: 10.1007/s00422-021-00864-y. Epub 2021 Mar 3. Biol Cybern. 2021. PMID: 33656573 Free PMC article.
References
-
- Ausborn Jessica, Koizumi Hidehiko, Barnett William H., John Tibin T., Zhang Ruli, Molkov Yaroslav I., Smith Jeffrey C., Rybak Ilya A. Organization of the core respiratory network: Insights from optogenetic and modeling studies. PLOS Computational Biology. 2018;14(4):e1006148. doi: 10.1371/journal.pcbi.1006148. - DOI - PMC - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

