Rotational-symmetry in a 3D scene and its 2D image
- PMID: 31239585
- PMCID: PMC6591714
- DOI: 10.1016/j.jmp.2018.10.001
Rotational-symmetry in a 3D scene and its 2D image
Abstract
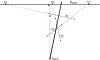
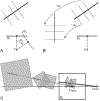
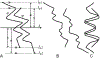
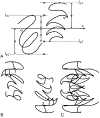
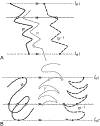
A 3D shape of an object is N-fold rotational-symmetric if the shape is invariant for 360/N degree rotations about an axis. Human observers are sensitive to the 2D rotational-symmetry of a retinal image, but they are less sensitive than they are to 2D mirror-symmetry, which involves invariance to reflection across an axis. Note that perception of the mirror-symmetry of a 2D image and a 3D shape has been well studied, where it has been shown that observers are sensitive to the mirror-symmetry of a 3D shape, and that 3D mirror-symmetry plays a critical role in the veridical perception of a 3D shape from its 2D image. On the other hand, the perception of rotational-symmetry, especially 3D rotational-symmetry, has received very little study. In this paper, we derive the geometrical properties of 2D and 3D rotational-symmetry and compare them to the geometrical properties of mirror-symmetry. Then, we discuss perceptual differences between mirror- and rotational symmetry based on this comparison. We found that rotational-symmetry has many geometrical properties that are similar to the geometrical properties of mirror-symmetry, but note that the 2D projection of a 3D rotational-symmetrical shape is more complex computationally than the 2D projection of a 3D mirror-symmetrical shape. This computational difficulty could make the human visual system less sensitive to the rotational-symmetry of a 3D shape than its mirror-symmetry.
Figures


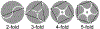



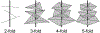







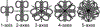
Similar articles
-
3D surface configuration modulates 2D symmetry detection.Vision Res. 2015 Feb;107:86-93. doi: 10.1016/j.visres.2014.12.007. Epub 2014 Dec 20. Vision Res. 2015. PMID: 25536469
-
A computational model that recovers the 3D shape of an object from a single 2D retinal representation.Vision Res. 2009 May;49(9):979-91. doi: 10.1016/j.visres.2008.05.013. Epub 2008 Jul 14. Vision Res. 2009. PMID: 18621410
-
Tensor based sparse decomposition of 3D shape for visual detection of mirror symmetry.Comput Methods Programs Biomed. 2012 Nov;108(2):629-43. doi: 10.1016/j.cmpb.2011.10.007. Epub 2011 Dec 12. Comput Methods Programs Biomed. 2012. PMID: 22169015
-
[Symmetry types, systems and multiplicity of the structure of adenovirus capsid. II. Rotational facet-groups of five-, three- and two-fold symmetry axes].Orv Hetil. 2006 Jan 8;147(1):15-24. Orv Hetil. 2006. PMID: 16519066 Review. Hungarian.
-
Mirrors are hard to break: A critical review and behavioral evidence on mirror-image processing in developmental dyslexia.J Exp Child Psychol. 2017 Jul;159:66-82. doi: 10.1016/j.jecp.2017.02.003. Epub 2017 Mar 9. J Exp Child Psychol. 2017. PMID: 28285044 Review.
Cited by
-
Commentary: Rectangularity is stronger than symmetry in interpreting 2D pictures as 3D objects.Front Hum Neurosci. 2023 Mar 24;17:1138287. doi: 10.3389/fnhum.2023.1138287. eCollection 2023. Front Hum Neurosci. 2023. PMID: 37033905 Free PMC article. No abstract available.
References
-
- Barlow HB, & Reeves BC (1979). The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vision Research, 19, 783–793. - PubMed
-
- Biederman I (1987). Recognition-by-components: A theory of human image understanding. Psychological Review, 94, 115–147. - PubMed
-
- Biederman I & Gerhardstein PC (1993). Recognizing depth-rotated objects: Evidence and conditions for three-dimensional viewpoint invariance. Journal of Experimental Psychology: Human Perception and Performance, 19, 1162–1182 - PubMed
-
- Binford T (1971). Visual perception by computer. IEEE Conference on Systems and control, Vol. 261,p. 262.
-
- Bingham GP & Muchisky MM (1993a). Center of mass perception and inertial frames of reference. Perception & Psychophysics, 54, 617–632. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
