The Notched Stick, an ancient vibrot example

Abstract

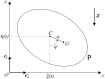
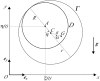
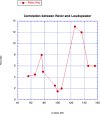
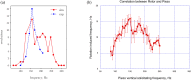
An intriguing simple toy, commonly known as the Notched Stick, is discussed as an example of a "vibrot", a device designed and built to yield conversion of mechanical vibrations into a rotational motion. The toy, that can be briefly described as a propeller fixed on a stick by means of a nail and free to rotate around it, is investigated from both an experimental and a numerical point of view, under various conditions and settings, to investigate the basic working principles of the device. The conversion efficiency from vibration to rotational motion turns out to be very small, or even not detectable at all, whenever the propeller is tightly connected to the stick nail and perfectly axisymmetrical with respect to the nail axis; the small effects possibly observed can be ascribed to friction forces. In contrast, the device succeeds in converting vibrations into rotations when the propeller center of mass is not aligned with the nail axis, a condition occurring when either the nail-propeller coupling is not tight or the propeller is not completely axisymmetrical relative to the nail axis. The propeller rotation may be induced by a process of parametric resonance for purely vertical oscillations of the nail, by ordinary resonance if the nail only oscillates horizontally or, finally, by a combination of both processes when nail oscillations take place in an intermediate direction. Parametric resonance explains the onset of rotations also when the weight of the propeller is negligible. In contrast with what is commonly claimed in the literature, the possible elliptical motion of the nail, due to a composition of two harmonic motions of the same frequency imposed along orthogonal directions, seems unnecessary to determine the propeller rotation.

Fig 1. Some examples of Notched Stick.

The typical appearance of the Notched Stick (NS): (from the top) a commercial one completely wood made; a NS with a rectangular stick and a plastic rotor without a microbearing; a NS mounted on a piezo, consisting of a square stick and a plastic rotor endowed with a microbearing.

Fig 2. Simple model with tight nail-propeller coupling.

A simple model of the device in the case of a tight nail-propeller coupling. C denotes the nail position in the vertical plane Oxy, whose coordinates (ξ,η) vary according to a given time law. G is the projection on the same plane of the center of mass of the propeller P. Finally, a stands for the (typically small) distance of G from the nail axis and φ is the rotation angle of the propeller. Constraints are assumed to be ideal, but allowance is made for energy dissipation by a viscous term $D_{\phi }=-\beta \stackrel{·}{\phi }$ proportional to the angular velocity of the propeller, moving in air.

Fig 3. Simple model with loose nail-propeller coupling.

A light pitchless propeller loosely mounted at the end of the rod by a nail to rotate freely. Another model of the device more appropriate for the case of a loose nail-propeller coupling. In the vertical plane Oxy the nail is represented by a rigid disk D of center A and radius R, animated by a purely translational motion whose description is given in terms of the varying coordinates ξ(t), η(t) of A. The inner edge of the propeller hole, represented by the rigid circular ring Γ of radius r and center C, is assumed to roll without slipping on the outer profile of the nail D. Pure rolling requires static friction between Γ and D, but it does not invalidate the assumption of ideal constraints. The moment of inertia of the propeller with respect to the axis passing through its center of mass and orthogonal to Oxy is supposed to be known. The orthogonal projection G of the center of mass on the plane Oxy may not coincide with the center C of the ring Γ, as described by the distance a and the angle α. The propeller rotation is parametrized by the angle φ.

Fig 4. Experimental setup.

The experimental setup of the system, with the notched stick (1) mounted on the loudspeaker (2) and endowed with a polyurethane propeller (3).

Fig 5. Experimental results for the loudspeaker vibration source.

Rotor frequency vs. loudspeaker frequency for a notched stick mounted on a loudspeaker and with a free moving microbearing.

Fig 6. Experimental results for the piezo vibration source and comparison with simulations.

(a) Comparison between some experimental and simulated data for a Notched Stick with a plastic rotor on a free moving microbearing mounted on a piezo vibratory device. Revolution frequency of the propeller as a function of excitation frequency. Each point corresponds to a single run of the experiment or the numerical simulation. The range of excitation frequencies at which the propeller rotates is similar for experimental and simulated tests. (b) Experimental data for a Notched Stick with a plastic rotor on a free moving microbearing mounted on a piezo vibratory device. Revolution frequency of the propeller as a function of excitation frequency in a larger interval than in Fig 6A. Repeated experiments allow to estimate the standard deviation of rotation frequency; the error on the imposed piezo frequency is negligible. The use of a piezo vibration source makes it possible a better control of the vibration plane. The data confirm the frequency peak at about 156 Hz and show a qualitative agreement with the simulated results of Fig 6A. Discrepancies in the experimental results of Fig 6A and 6B are probably due to the circumstance that, for technical reasons, between the two sets of measurements the apparatus had to be dismounted and the restored again (re-use of the antivibrating table for other purposes). The unavoidable aging of wood and polyurethane components, induced by the many operations carried out on the device, may also have played a minor role.

Fig 7. Displacement of the nail head.

Displacement of the center of the nail head measured from the recording of an experiment performed stimulating the Notched Stick through the piezoelectrical device applying 156Hz frequency. Dots are the measured data and solid lines the sinusoidal fit.

Fig 8. Geometrical model of the Notched Stick for simulations.

The geometrical model of the Notched Stick adopted in multibody dynamics simulations consisting of the propeller, the nail, the microbearing and an additional part, preventing the propeller disengagement.

Fig 9. Phase portraits.

Phase portrait of the propeller. As in the case of the simple pendulum, when the propeller does not rotate, e.g. at 65 Hz (left), the diagram shows the trend of a closed curve. In contrast, the trend of the diagram at 156 Hz is that of an open curve (right), due to the revolution of the propeller; the final stage of the run appears rather noisy, probably owing to nail/propeller shocks and relative slip, that sometimes may suddenly enhance friction forces and angular speed variations. Unfortunately, the backlash between the nail and the propeller turns out to be necessary to the onset of rotations, but it also makes the dynamics of the system far form being trivial.