Spatial Lymphocyte Dynamics in Lymph Nodes Predicts the Cytotoxic T Cell Frequency Needed for HIV Infection Control

Abstract

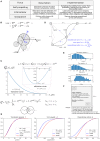
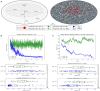
The surveillance of host body tissues by immune cells is central for mediating their defense function. In vivo imaging technologies have been used to quantitatively characterize target cell scanning and migration of lymphocytes within lymph nodes (LNs). The translation of these quantitative insights into a predictive understanding of immune system functioning in response to various perturbations critically depends on computational tools linking the individual immune cell properties with the emergent behavior of the immune system. By choosing the Newtonian second law for the governing equations, we developed a broadly applicable mathematical model linking individual and coordinated T-cell behaviors. The spatial cell dynamics is described by a superposition of autonomous locomotion, intercellular interaction, and viscous damping processes. The model is calibrated using in vivo data on T-cell motility metrics in LNs such as the translational speeds, turning angle speeds, and meandering indices. The model is applied to predict the impact of T-cell motility on protection against HIV infection, i.e., to estimate the threshold frequency of HIV-specific cytotoxic T cells (CTLs) that is required to detect productively infected cells before the release of viral particles starts. With this, it provides guidance for HIV vaccine studies allowing for the migration of cells in fibrotic LNs.

Keywords: HIV infection; cell motility; cytotoxic T cell scanning; dissipative particle dynamics; lymphoid tissue; multicellular dynamics; stochastic differential equation.

Figure 1

Physics-based model of multicellular system dynamics reproduces experimental data on T-cell locomotion. (A) The set of forces considered in the model with description of their features and implementation details. (B) The fundamental equation governing locomotion of cells determined by the forces exerted on cell i, including the repulsive–attractive interaction with neighbor cells p and k, respectively. (C) The parameterization of intercellular interaction force $f_{\mathrm{\text{ij}}}^{\mathrm{\text{int}}}$and formula definition. The calibrated force for non-specific interaction of two T cells with a radius of 3 μm is depicted. By simulation, the parameters a and b are calculated at each time step depending on the radii r_i, r_j and the distances h_ij, x, so that the condition $f_{ij}(\lambda r_j)=f_{ij}(r_j)=0,min{f}_{ij}(x)=-f_i^{adh}$ is satisfied. The parameter λ determines the relative deformation of the cells that separates the repulsive and attractive interactions between them. Parameter $f_i^{adh}$ represents the adhesive strength between the membranes of cells i and j. (D) Schematic illustration and definition of the metrics characterizing T-cell motility: translational speed, turning angle speed, and meandering index. All metrics are measured for each cell every Δt seconds and pooled together to form statistical distributions. (E) Statistical profiles characterizing the T-cell locomotion consists of distribution histograms of translational speeds, turning angle speeds, and meandering indices. The histograms are derived from the corresponding empirical cumulative distribution functions (CDFs) available in Figure S17 from Read et al. (22), in which original in vivo data are presented. (F) The details of the 2D geometric setup for simulations used in the model calibration: spatial configuration, initial and boundary conditions, and the experimental protocol used to sample the statistical profile. (G) The statistical characteristics of T-cell motility coming from simulations of the calibrated model plotted against the in vivo histogram data (22). The statistical distributions of each metric are depicted as CDFs. The Kolmogorov–Smirnov statistics comparing the model and target CDFs are indicated with their respective p-values.

Figure 2

Heterogeneous dynamics of T cells in LNs. (A) The scheme of a LN and illustration of the initial configuration generated for simulations. DCs, CD4⁺ T cells, and CD8⁺ T cells are placed within a LN as described in the Supplementary Text with total cellularity of 12,469 cells, ≈ 80% packing density and ≈ 1% precursor frequency. (B) Twelve-hour kinetics of median velocities of antigen-specific CD8⁺ T and CD4⁺ T cells, and their distributions at the start and at the end of a 12-h simulation. (C) Twelve-hour kinetics of median distances from T cells to the centroid of DCs, measured for antigen-specific CD8⁺ T and CD4⁺ T cells, and their distributions at the start and at the end of a 12-h simulation. TC, T cell; DC, dendritic cell.

Figure 3

Quantitation of immune cell motility, driving forces, and contacts. (A) Representative example of individual cell trajectories obtained with numerical realization of the calibrated model. The trajectories illustrate the 5-h dynamics of 15 cells randomly chosen from 4,489 cells presented in the 412 ×412 μm² domain with periodic boundary conditions. (B) Twelve-hour multicellular dynamics of T-cell trajectories in a lymph node obtained by numerical simulation with an initial configuration specified in Figure 2A. Only cells with total displacement longer than 27 μm are shown. (C) Values of forces and cell velocities driving the multicellular system dynamics in a square subdomain of a LN. In a center pane, the velocity field is represented as a contour plot of the field of cell velocity magnitudes linearly interpolated at uniform grid, as well as detected streamlines of possible cell flow patterns. (D) Kinetics of the numbers of cognate DC–T cell contacts at different stages of the simulation and distribution of durations of all cognate contact durations occurring within a 12-h simulation. DC, dendritic cell.

Figure 4

Conditions to locate HIV-infected target cells within a LN before viral release. (A) General scheme of in silico simulations. Time since the HIV-infected target cell was introduced until it was located by effector HIV-specific CTLs was measured in 24-h simulations. The infected cell was either non-motile DC (B,D) or motile CD4⁺ T cell (C,E). In (B,C), the precursor frequency, i.e., the frequency of effector T cells, was varied, from 0.04 to 5%. In (D,E), the effect of decreased intrinsic motility of T cells was studied. The average T-cell velocity was decreased up to 50%. In all plots, the fraction of cases with location time >24 h is indicated, thus providing the estimates for probability to locate target cells within 24 h. The time range between the start and the peak HIV release from infected T cells (20) is shown in pink. It is used to estimate the probability of a virus burst to escape effector CTLs and, thus, to contribute to the spread of HIV-infected cells within a LN. TC, T cell; DC, dendritic cell.