Application of Graph Theory for Identifying Connectivity Patterns in Human Brain Networks: A Systematic Review
- PMID: 31249501
- PMCID: PMC6582769
- DOI: 10.3389/fnins.2019.00585
Application of Graph Theory for Identifying Connectivity Patterns in Human Brain Networks: A Systematic Review
Abstract
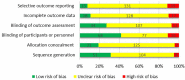
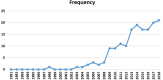
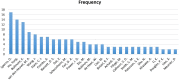
Background: Analysis of the human connectome using functional magnetic resonance imaging (fMRI) started in the mid-1990s and attracted increasing attention in attempts to discover the neural underpinnings of human cognition and neurological disorders. In general, brain connectivity patterns from fMRI data are classified as statistical dependencies (functional connectivity) or causal interactions (effective connectivity) among various neural units. Computational methods, especially graph theory-based methods, have recently played a significant role in understanding brain connectivity architecture. Objectives: Thanks to the emergence of graph theoretical analysis, the main purpose of the current paper is to systematically review how brain properties can emerge through the interactions of distinct neuronal units in various cognitive and neurological applications using fMRI. Moreover, this article provides an overview of the existing functional and effective connectivity methods used to construct the brain network, along with their advantages and pitfalls. Methods: In this systematic review, the databases Science Direct, Scopus, arXiv, Google Scholar, IEEE Xplore, PsycINFO, PubMed, and SpringerLink are employed for exploring the evolution of computational methods in human brain connectivity from 1990 to the present, focusing on graph theory. The Cochrane Collaboration's tool was used to assess the risk of bias in individual studies. Results: Our results show that graph theory and its implications in cognitive neuroscience have attracted the attention of researchers since 2009 (as the Human Connectome Project launched), because of their prominent capability in characterizing the behavior of complex brain systems. Although graph theoretical approach can be generally applied to either functional or effective connectivity patterns during rest or task performance, to date, most articles have focused on the resting-state functional connectivity. Conclusions: This review provides an insight into how to utilize graph theoretical measures to make neurobiological inferences regarding the mechanisms underlying human cognition and behavior as well as different brain disorders.
Keywords: brain connectivity; brain networks; connectome; effective connectivity; fMRI; functional connectivity; graph theory; small-world.
Figures

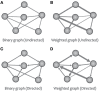
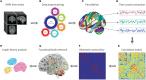


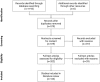
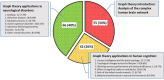

References
-
- Albert M. S., DeKosky S. T., Dickson D., Dubois B., Feldman H. H., Fox N. C., et al. . (2011). The diagnosis of mild cognitive impairment due to Alzheimer's disease: Recommendations from the National Institute on Aging-Alzheimer's Association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimers Dement. 7, 270–279. 10.1016/j.jalz.2011.03.008 - DOI - PMC - PubMed
-
- Algunaid R. F., Algumaei A. H., Rushdi M. A., Yassine I. A. (2018). Schizophrenic patient identification using graph-theoretic features of resting-state fMRI data. Biomed. Signal Process. Control 43, 289–299. 10.1016/j.bspc.2018.02.018 - DOI
Publication types
LinkOut - more resources
Full Text Sources

