S3CMTF: Fast, accurate, and scalable method for incomplete coupled matrix-tensor factorization

Abstract

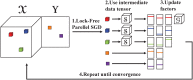
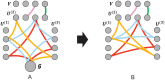
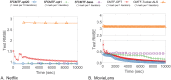
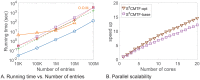
How can we extract hidden relations from a tensor and a matrix data simultaneously in a fast, accurate, and scalable way? Coupled matrix-tensor factorization (CMTF) is an important tool for this purpose. Designing an accurate and efficient CMTF method has become more crucial as the size and dimension of real-world data are growing explosively. However, existing methods for CMTF suffer from lack of accuracy, slow running time, and limited scalability. In this paper, we propose S3CMTF, a fast, accurate, and scalable CMTF method. In contrast to previous methods which do not handle large sparse tensors and are not parallelizable, S3CMTF provides parallel sparse CMTF by carefully deriving gradient update rules. S3CMTF asynchronously updates partial gradients without expensive locking. We show that our method is guaranteed to converge to a quality solution theoretically and empirically. S3CMTF further boosts the performance by carefully storing intermediate computation and reusing them. We theoretically and empirically show that S3CMTF is the fastest, outperforming existing methods. Experimental results show that S3CMTF is up to 930× faster than existing methods while providing the best accuracy. S3CMTF shows linear scalability on the number of data entries and the number of cores. In addition, we apply S3CMTF to Yelp rating tensor data coupled with 3 additional matrices to discover interesting patterns.

Fig 1. Comparison of our proposed S³CMTF and the existing methods.

(a) For a fixed number of nonzeros, S³CMTF takes constant time as dimensionality grows, while existing methods become slower. Our sequential method S³CMTF-opt1 is 930× and 54× faster than CMTF-OPT and CMTF-Tucker ALS, respectively. (b) S³CMTF-opt20 shows the best convergence rate and accuracy on real world Yelp dataset. CMTF-Tucker-ALS shows O.O.M. in both experiments. (O.O.M.: out of memory error).

Fig 2. The scheme for S³CMTF.

Fig 3. Example hypergraphs induced by S³CMTF objective function (Eq (7)).

A matrix Y is coupled to the second mode of $\mathcal{X}$ with a coupled factor matrix V. Each node represents a factor row or the core tensor. Each hyperedge includes corresponding factors to an SGD update. (a) Induced hypergraph with the core tensor. Every hyperedge corresponding to tensor entries includes $\mathcal{G}$. (b) Induced hypergraph without core tensor. The graph has sparse structure as every node is shared by only few hyperedges.

Fig 4. Test RMSE of S³CMTF and other CMTF methods over iterations.

S³CMTF-opt20 shows the best convergence rate and accuracy.

Fig 5. Comparison with SALS-single for movieLens dataset.

We compare two non-coupled version of S³CMTF, S³CMTF-CP-opt and S³CMTF-TUCKER-opt with the parallel CP decomposition method, SALS-single. For (a), we set 1 mark per 20 iterations for clarity. (a) S³CMTF converges faster to a lower error than SALS does. (b) S³CMTF-CP-opt is 2.3× faster than SALS-single.

Fig 6. Comparison of scalability.

(a) S³CMTF shows linear scalability as the number of entries increases. (b) S³CMTF-base and S³CMTF-opt show linear speed up as the number of cores grows. O.O.M.: out of memory error.

Fig 7

(a) Gap statistics on U⁽²⁾ of S³CMTF and the Tucker decomposition for Yelp dataset. S³CMTF outperforms the naive Tucker decomposition for its clustering ability. (b) Visualization of the personal recommendation scenario.