Recent advancements on the phase field approach to brittle fracture for heterogeneous materials and structures

Abstract

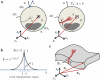
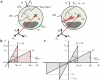
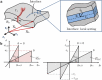
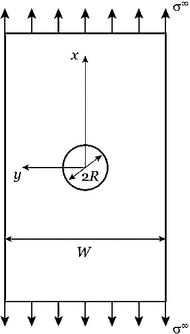
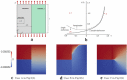
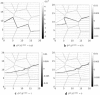
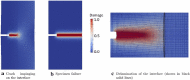
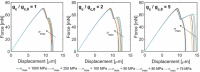
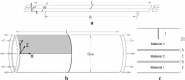
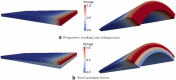
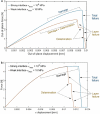
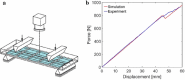
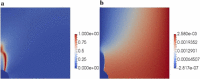
Recent advancements on the variational approach to fracture for the prediction of complex crack patterns in heterogeneous materials and composite structures is herein proposed, as a result of the frontier research activities undertaken in the FP7 ERC Starting Grant project CA2PVM which focuses on the development of computational methods for the durability and the reliability assessment of photovoltaic laminates. From the methodological viewpoint, the phase field approach to describe the propagation of brittle fracture in the bulk has been coupled for the very first time with the cohesive zone model to depict interface crack growth events, for 2D isotropic and anisotropic constitutive laws, and also for 3D finite elasticity. After a summary of the key aspects underlying the theoretical formulation and the finite element implementation using a monolithic fully implicit solution scheme, an overview of the main technological applications involving layered shells, interface mechanical problems and polycrystalline materials is provided. The examples are selected to show the capability of the proposed approach to investigate complex phenomena such as crack deflection vs. crack penetration at an interface, intergranular vs. transgranular crack growth in polycrystals, and interlayer vs. translayer failure in laminates.

Keywords: Cohesive zone model; Heterogeneous materials; Nonlinear finite element method; Phase field model of fracture; Solid shell.

Fig. 1

a Comparison between the discrete discontinuity of the LEFM theory (left) with the smeared discontinuity of the PF model (right); b 1D approximation function which smear out the discontinuity, the damage $\mathfrak{d}$ follows the exponential based function $\mathfrak{d}={\text{e}}^{-\mid x\mid /l}$. c Phase field approach for thin-walled structures adopting the solid shell approach

Fig. 2

a Coexistence between brittle fracture in the bulk and cohesive debonding of an interface within the context of the phase field approach of fracture. Schematic representation of the traction separation law of the CZM which accounts for the phase field variable. b Mode I CZM traction $\sigma$ vs. $g_n$. c Mode II CZM traction $\tau$ vs. $g_t$

Fig. 3

a Generic shell body with cracks and prescribed interfaces; b traction–separation laws for fracture Modes I and II

Fig. 4

Geometry of the simulated open-hole lamina (from [51])

Fig. 5

a Experimental and numerical remote stress vs. displacement curves; b experimental–numerical crack path for open-hole specimens

Fig. 6

Tearing test. a Geometry and loading condition of the test; b crack propagation; c specimen failure (from [24])

Fig. 7

Tensile test of a cylindrical shell. a Geometry and loading condition of the test; b crack propagation; c specimen failure (from [24])

Fig. 8

a Geometry considered to study the effect of a crack impinging on an interface; b curve which separate the crack penetration and deflection cases for different impinging angles; transition from crack deflection, c to crack penetration, d for a brittle interface $({\mathrm{\Pi }}_2\to 0)$ with angle $\theta ={30}^{\circ }$ (from [37])

Fig. 9

a Geometry of the tensile test of a bi-material system; b curve which separate the crack penetration, crack single deflection and crack double deflection cases; transition from double deflection (c) to single deflection (d) and crack penetration (e) for a brittle interface $({\mathrm{\Pi }}_2\to 0)$ varying the ratio $1/{\mathrm{\Pi }}_1$. The contour plots scale is a dimensional vertical displacement (from [37])

Fig. 10

Finite element mesh of the polycrystalline silicon photovoltaic cell. The specimen has a notch on the left edge. The grain orientations are specified by the Miller indices in the grains and by the different colours (from [51])

Fig. 11

Contour plots of inelastic displacement field, illustrating the crack path for different values of ${\mathcal{G}}^{\mathit{gb}}/{\mathcal{G}}^{⟨100⟩}$ (from [51])

Fig. 12

a, b Two steps of crack propagation; c close-up view of delamination when the crack is approaching the interface (from [47])

Fig. 13

Force displacement curve for different ${\sigma }_{\text{max}}$ and different ratio $g_{\text{c}}/g_{\text{c,0}}$ (from [47])

Fig. 14

Geometry of the 4-point-bending specimen in a and geometry of the cylinder under tension in b. Composite composition through the thickness in c (from [47])

Fig. 15

Crack propagation and delamination in a notched sandwich panel. a Flat geometry under tensile and 4-point banding loading; b cylindrical geometry under tensile loading (from [47])

Fig. 16

Force-displacement curves. a Sandwich panel under tension and 4-point-bending, b Sandwich cylinder under tension (from [47])

Fig. 17

4-point bending test of a photovoltaic panel. a Experimental test setup, b force displacement curve (from [47])

Fig. 18

Micromechanics of fibre reinforced composite materials: geometry and boundary conditions

Fig. 19

Micromechanics of fibre reinforced composite materials: stress–strain evolution curve and damage pattern at different stages of the simulation

Fig. 20

Micromechanics of fibre reinforced composite materials: a final damage pattern. b Final horizontal displacement