Self-Sustained Cascading Coalescence in Surface Condensation

Abstract

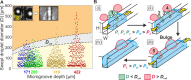
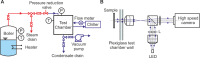
Sustained dropwise condensation of water requires rapid shedding of condensed droplets from the surface. Here, we elucidate a microfluidic mechanism that spontaneously sweeps condensed microscale droplets without the need for the traditional droplet removal pathways such as use of superhydrophobicity for droplet rolling and jumping and utilization of wettability gradients for directional droplet transport among others. The mechanism involves self-generated, directional, cascading coalescence sequences of condensed microscale droplets along standard hydrophobic microgrooves. Each sequence appears like a spontaneous zipping process, can sweep droplets along the microgroove at speeds of up to ∼1 m/s, and can extend for lengths more than 100 times the microgroove width. We investigate this phenomenon through high-speed in situ microscale condensation observations and demonstrate that it is enabled by rapid oscillations of a condensate meniscus formed locally in a filled microgroove and pinned on its edges. Such oscillations are in turn spontaneously initiated by coalescence of an individual droplet growing on the ridge with the microgroove meniscus. We quantify the coalescence cascades by characterizing the size distribution of the swept droplets and propose a simple analytical model to explain the results. We also demonstrate that, as condensation proceeds on the hydrophobic microgrooved surface, the coalescence cascades recur spontaneously through repetitive dewetting of the microgrooves. Lastly, we identify surface design rules for consistent realization of the cascades. The hydrophobic microgrooved textures required for the activation of this mechanism can be realized through conventional, scalable surface fabrication methods on a broad range of materials (we demonstrate with aluminum and silicon), thus promising direct application in a host of phase-change processes.

Keywords: cascade; coalescence; condensation; hydrophobic; microgrooves.

Figure 1

(A) Microgroove machined in aluminum and coated with polytetrafluoroethylene (PTFE). (B) Hydrophobicity of the microgroove toward condensed microdroplets as observed in ESEM. The vapor pressure was set at 0.87 kPa, and the cooling stage was set at 2 °C. (See the Supporting Information for details on ESEM observations.)

Figure 2

Microdroplet coalescence cascade. (A) High-speed microdroplet coalescence sequence along a ∼100 μm wide and ∼200 μm deep hydrophobic microgroove. Substrate: aluminum; coating: polytetrafluoroethylene (PTFE). The yellow color indicates the coalescence cascade progress. g indicates gravity. The scale bar represents 200 μm. Images are captured at 10,000 fps (frames per second) (Movie S1). (B) High-speed snapshots captured at 250,000 fps demonstrating the spontaneous initiation and sustenance of the coalescence sequence. The scale bar represents 100 μm. The white arrow indicates the viewing direction for (C). (See the Experimental Section and Section S2 for details of the experimental setup and procedure.) (C) Schematics corresponding to images in (B). Droplet 1 spontaneously coalesces with the condensate meniscus pinned at microgroove edges and initiates the coalescence sequence [see yellow arrows in panel ii in (B) and (C)]. As this coalescence proceeds, the meniscus rises [by amplitude as shown in the inset figure in panel iii of (C)]. This appears as a capillary ripple traveling along the microgroove meniscus [panels ii–iv in (B)]. The oscillating meniscus first catches droplets 2 and 3 [green arrows in panel v in (B) and (C)], which in turn triggers the coalescence of droplet 4 [pink arrows in panel vi in (B) and (C)] thus propagating the coalescence sequence. (Movie S2.)

Figure 3

(A) Beeswarm distribution plots of swept droplet diameters (D, defined in inset) for microgrooves of widths of ∼100 μm and depths of ∼171 to 422 μm machined in aluminum and coated with PTFE. The grey zone demarcates the limit estimate D_crit. Each beeswarm plot is based on ∼300 measurements and is shown in different colors for clarity. In the beeswarm distribution, the horizontal spread at any ordinate D indicates the relative proportion of droplets of diameter D swept by the cascading coalescence sequence. The yellow zone below the D_crit limit represents the range of droplet sizes swept by the coalescence sequence progressing in a partially filled microgroove. The orange zone above D_crit indicates droplet sizes swept by the coalescence sequence proceeding in a completely filled microgroove or in the presence of a large bulge. (B) Schematic illustrating that droplets with D < D_crit (droplets 1, 2, and 3 in green) are readily absorbed by the advancing meniscus [panels (i) and (ii)] due to a favorable Laplace pressure difference with the microgroove meniscus (P₁, P₂, P₃ > P_M). A droplet with D > D_crit (droplet 4 in red with P₄ < P_M) forms a bulge. The bulge causes the sweeping of subsequent droplets with D > D_crit [e.g., droplet 5 in panels (iii) and (iv)]. P_B represents Laplace pressures inside the bulge. The legend at the bottom defines the color scheme for droplets.

Figure 4

Periodicity of the zipping-like cascading coalescence sequence: (A) a single bulge and filled microgroove are formed after the conclusion of the coalescence sequence (panel i). Subsequently, the bulge induces dewetting of the microgroove through condensate withdrawal as indicated by yellow arrows. Scale bar: 200 μm. Images are captured at 1000 fps. (B) Schematic showing the condensate withdrawal process along with an overall pressure difference driving this process. (C) Zoomed-out view of the sample wherein the coalescence cascades are visible as intermittent dark ridge areas. Three bulges formed due to such events are encircled in panel (ii). These bulges grow due to repeated occurrences of the effect and coalescence with more droplets. Eventually, the resulting large drops [encircled in panel (iii)] are shed under gravity as indicated by yellow arrows. Drop 1 also moves under gravity initially but is eventually absorbed into the microgroove when it gets connected to a large drop pinned at the edge of the sample via a filled microgroove (panels vii and viii). Scale bar: 2 mm. Substrate: aluminum. Coating: PTFE. Images are captured at 50 fps.

Figure 5

(A) Regime map of the liquid zipping-like coalescence sequence with varying aspect ratios (H/W) and a fixed ridge width for hydrophobic microgrooves in aluminum. The numbers in green and red indicate aspect ratios for the various microgroove geometries. The green data points correspond to microgrooves for which the coalescence sequence is realized and red data points represent microgrooves where the coalescence sequence is absent. The contour lines correspond to the ratio [D_crit cos (θ – π/2)]/L. Ridge width L is defined in the inset of (B). Based on data points and contours, the microgrooves need to be designed such that (H/W) > 1.6 and [D_crit cos (θ – π/2)]/L > 0.3. (B) Control of swept droplet size through reduction in microgroove ridge width L. Beeswarm distributions of swept droplet diameters are shown in terms of base diameter D cos (θ – π/2) for ∼100 μm wide and ∼200 μm deep microgrooves for ridge widths L of ∼480 and ∼240 μm (in blue), ∼180 μm (in black), and ∼90 μm (in orange). D_crit cos (θ – π/2) for this microgroove geometry lies in the range of ∼164–216 μm as indicated by the grey zone. For L > D_crit cos (θ – π/2), swept droplet distributions (in blue) are unaffected by L. However as L is reduced, the swept droplet distribution first becomes more uniform [see distribution in black for L ≈ D_crit cos (θ – π/2)], and subsequently, the maximum droplet swept size is reduced when L < D_crit cos (θ – π/2) (see distribution in orange).

Figure 6

(A) Schematic of the experimental setup to induce condensation on the test sample. (B) Optical setup for high-speed, high-magnification observation of the domino effect. The lens L, shown as dashed lines, was removed for imaging at high frame rates.