Wavefront sensing at X-ray free-electron lasers

Abstract

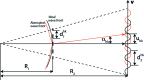
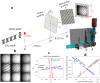
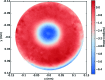
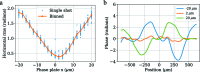
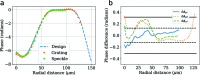
Here a direct comparison is made between various X-ray wavefront sensing methods with application to optics alignment and focus characterization at X-ray free-electron lasers (XFELs). Focus optimization at XFEL beamlines presents unique challenges due to high peak powers as well as beam pointing instability, meaning that techniques capable of single-shot measurement and that probe the wavefront at an out-of-focus location are desirable. The techniques chosen for the comparison include single-phase-grating Talbot interferometry (shearing interferometry), dual-grating Talbot interferometry (moiré deflectometry) and speckle tracking. All three methods were implemented during a single beam time at the Linac Coherent Light Source, at the X-ray Pump Probe beamline, in order to make a direct comparison. Each method was used to characterize the wavefront resulting from a stack of beryllium compound refractive lenses followed by a corrective phase plate. In addition, difference wavefront measurements with and without the phase plate agreed with its design to within λ/20, which enabled a direct quantitative comparison between methods. Finally, a path toward automated alignment at XFEL beamlines using a wavefront sensor to close the loop is presented.

Keywords: X-ray free-electron lasers; grating interferometry; speckle tracking; wavefront sensing.

Figure 1

Photographs of the experimental setup. The X-ray beam was focused by a set of beryllium CRL lenses (a) and a phase plate with horizontal and vertical degrees of freedom was placed downstream of the CRL optics. The grating/speckle phase modulators were mounted on a motorized positioner with long travel range along the optical axis (b). Two indirect X-ray detectors (c) with YAG scintillating screens were placed further downstream at approximately 2 m distance from the focus, and the compact moiré interferometer was mounted as the last part of the setup (d).

Figure 2

Operation principle of the single-phase-grating method for wavefront shape measurement; v is the unit vector in the direction of q _hk.

Figure 3

The π and π/2 phase gratings used in the single-phase-grating setup. (a) Si π grating, d ₁ = 2.725 µm, height h = 11 µm; (b) Si π grating, d ₁ = 14.142 µm, h = 12 µm; (c,d) CVD diamond π/2 phase grating, d ₁ = 2.282 µm, h = 2.932 µm.

Figure 4

Comparison of visibility variation along the optical axis for basic (45° and 125° direction) and mixed harmonics (0° and 90° direction) for π/2 diamond (a) and π Si (d) phase checkerboard gratings. The pitch in the diagonal direction was 2.8 µm for the diamond grating and 2.725 µm for the Si grating. Vertical lines in the graphs represent the theoretical positions for the Talbot distances (black) and fractional Talbot distances for basic (red) and mixed (green) harmonics. The interferograms (b,c,e,f) shown are taken from the first maxima for the basic harmonics. The scale bar represents 100 µm. For the analysis of the visibility the area marked with red squares in (b) and (e) was used. The locations and sizes of these regions of interest were chosen for visibility analysis based on the nearly uniform illumination within these areas.

Figure 5

Distances calibration of Si π-phase shifting grating with diagonal pitch size 2.725 µm.

Figure 6

(a) Schematic layout of the moiré XGI experimental setup at the SLAC XPP beamline. The XFEL pulses with 9.5 keV photon energy are focused with a stack of 20 compound refractive lenses followed by a corrective phase plate for diffraction-limited focusing. The grating interferometer was installed further downstream, consisting of phase (P) and absorption (A) gratings. Red arrows indicate moiré fringe periods p _x and p _y extracted via two-dimensional Fourier analysis (see text). (b) Selected moiré interferograms measured by rotating the absorption grating; (c) with extracted moiré fringe frequencies p _x and p _y in the horizontal and vertical directions for calibration. (d) Angular calibration of the moiré XGI, vertical arrows indicate the relative β offset between the two gratings indicated in panel (a).

Figure 7

Flowchart of the moiré XGI algorithm with horizontally (a–f) and vertically (a′–f′) aligned line gratings (see text). (g) Lineout stack of wavefront errors in the vertical direction showing gradual improvement as the phase plate is moving toward the central position (0 µm). (h) Comparison of wavefront errors between moiré XGI [bottom line in (g)] and single-phase-grating Talbot interferometry (dashed line) at the central phase plate position (0 µm). The blue rectangle is marking the expected λ/4 wavefront error improvement compared with ∼1.5λ denoted by vertical segment in panel (g). (i) Vertical through-focus and focal plane intensity profile retrieved using amplitude and phase back-propagation. The amplitude profile extends over the first-order amplitude peak center in vertical direction, the related height profile is seen in panel (h). The vertical beam waist profile with ∼220 nm FWHM was extracted along the dashed segment.

Figure 8

Sketch of the experimental setup used to perform X-ray speckle tracking in absolute and differential mode. A speckle scatterer and two synchronized indirect X-ray detectors, the first one being semi-transparent, are aligned along the beam. For our experiment, the distances were fixed to: d ₁ = 905 mm, d ₂ = 1325 mm, R = 590 mm and f = 308 mm (see text for further details).

Figure 9

Recovered profile of the full phase plate, based on X-ray speckle tracking in differential mode. This shows the full contribution of the phase plate to the wavefront, spherical term included. Note that the plate was not well centered at this time.

Figure 10

Illustration of real-time processing for phase plate alignment. (a) An example of what can be seen live during the measurement. The root mean square of 1D horizontal lineouts of the aspheric phase are used to obtain a measure of the aberrations in the horizontal direction, which in this case are strongly affected by the relative alignment between the phase plate and CRLs. (b) Single-shot horizontal aspheric phase lineouts are shown for the first, optimal and last positions in the scan, which were −20 µm, 2 µm and 20 µm, respectively.

Figure 11

2D wavefront retrieval with and without the corrective phase plate, based on single FEL shots and using a π-phase checkerboard grating with 14.1 µm diagonal pitch. (a) Wavefront with phase plate aligned, with scale bar corresponding to 200 µm at the detection plane. (b) Wavefront with phase plate removed. (c) Recovered profile of phase plate, based on subtraction of (b) from (a). The colorbar at the right of (c) is shared among all three phase profiles. The intensity of the beam can also be extracted from the Talbot image (d), which in combination with the retrieved wavefront can be used to obtain profiles of the focus, without (e) and with (f) phase plate correction. From a visual inspection of (e) and (f) it can be seen that the phase plate removes most of the fourth-order spherical aberration, but does not compensate for the astigmatism that likely comes from the monochromator crystals. The scale bar in (f) corresponds to 500 nm and is shared with (e), and the colorbar at right of (f) is shared between (d)–(f).

Figure 12

(a) The radial profile of the phase plate was measured using both single-grating interferometry and X-ray speckle tracking in differential mode by making measurements of the wavefront, with and without the phase plate inserted, and performing an azimuthal average of the resulting 2D profile [see Fig. 11(c) ▸]. Since care was taken to process data with and without the phase plate in exactly the same way, the only fit parameter is a scaling of the radial coordinates. (b) A quantitative comparison can be made by examining the phase difference between the curves from (a). The curves labeled Δϕ_gs, Δϕ_gd and Δϕ_sd refer to differences between grating and speckle, grating and design, and speckle and design, respectively. The region between the solid horizontal lines corresponds to agreement within ±λ/20 and the region between the dashed horizontal lines corresponds to within ±λ/50.