Waveguide coupling via magnetic gratings with effective strips
- PMID: 31275624
- PMCID: PMC6604653
- DOI: 10.3390/app8040617
Waveguide coupling via magnetic gratings with effective strips
Abstract
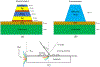
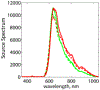
Gratings with complex multilayer strips are studied under inclined incident light. Great interest in these gratings is due to applications as input/output tools for waveguides and as subwavelength metafilms. The structured strips introduce anisotropy in the effective parameters, providing additional flexibility in polarization and angular dependences of optical responses. Their characterization is challenging in the intermediate regime between subwavelength and diffractive modes. The transition between modes occurs at the Wood's anomaly wavelength, which is different at different angle of incidence. The usual characterization with an effective film using permittivity ε and permeability μ has limited effectiveness at normal incidence but does not apply at inclined illumination, due to the effect of periodicity. The optical properties are better characterized with effective medium strips instead of an effective medium layer to account for the multilayer strips and the underlying periodic nature of the grating. This approach is convenient for describing such intermediate gratings for two types of applications: both metafilms and the coupling of incident waves to waveguide modes or diffraction orders. The parameters of the effective strips are retrieved by matching the spectral-angular map at different incident angles.
Keywords: homogenization; magnetic grating; metamaterials; metasurfaces; waveguide coupling.
Conflict of interest statement
Conflicts of Interest: The authors declare no conflict of interest.
Figures

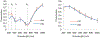


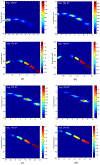
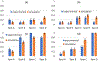
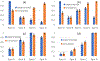

References
-
- Kildishev AV; Cai W; Chettiar UK; Yuan H-K; Sarychev AK; Drachev VP; Shalaev VM Negative refractive index in optics of metal-dielectric composites. JOSA B 2006, 23, 423–433, doi:10.1364/JOSAB.23.000423. - DOI
-
- Smith DR; Schultz S; Markoš P; Soukoulis CM Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 2002, 65,195104, doi:10.1103/PhysRevB.65.195104. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
