A computational model of induced pluripotent stem-cell derived cardiomyocytes incorporating experimental variability from multiple data sources
- PMID: 31278749
- PMCID: PMC6767694
- DOI: 10.1113/JP277724
A computational model of induced pluripotent stem-cell derived cardiomyocytes incorporating experimental variability from multiple data sources
Abstract
Induced pluripotent stem cell-derived cardiomyocytes (iPSC-CMs) capture patient-specific genotype-phenotype relationships, as well as cell-to-cell variability of cardiac electrical activity Computational modelling and simulation provide a high throughput approach to reconcile multiple datasets describing physiological variability, and also identify vulnerable parameter regimes We have developed a whole-cell model of iPSC-CMs, composed of single exponential voltage-dependent gating variable rate constants, parameterized to fit experimental iPSC-CM outputs We have utilized experimental data across multiple laboratories to model experimental variability and investigate subcellular phenotypic mechanisms in iPSC-CMs This framework links molecular mechanisms to cellular-level outputs by revealing unique subsets of model parameters linked to known iPSC-CM phenotypes ABSTRACT: There is a profound need to develop a strategy for predicting patient-to-patient vulnerability in the emergence of cardiac arrhythmia. A promising in vitro method to address patient-specific proclivity to cardiac disease utilizes induced pluripotent stem cell-derived cardiomyocytes (iPSC-CMs). A major strength of this approach is that iPSC-CMs contain donor genetic information and therefore capture patient-specific genotype-phenotype relationships. A cited detriment of iPSC-CMs is the cell-to-cell variability observed in electrical activity. We postulated, however, that cell-to-cell variability may constitute a strength when appropriately utilized in a computational framework to build cell populations that can be employed to identify phenotypic mechanisms and pinpoint key sensitive parameters. Thus, we have exploited variation in experimental data across multiple laboratories to develop a computational framework for investigating subcellular phenotypic mechanisms. We have developed a whole-cell model of iPSC-CMs composed of simple model components comprising ion channel models with single exponential voltage-dependent gating variable rate constants, parameterized to fit experimental iPSC-CM data for all major ionic currents. By optimizing ionic current model parameters to multiple experimental datasets, we incorporate experimentally-observed variability in the ionic currents. The resulting population of cellular models predicts robust inter-subject variability in iPSC-CMs. This approach links molecular mechanisms to known cellular-level iPSC-CM phenotypes, as shown by comparing immature and mature subpopulations of models to analyse the contributing factors underlying each phenotype. In the future, the presented models can be readily expanded to include genetic mutations and pharmacological interventions for studying the mechanisms of rare events, such as arrhythmia triggers.
Keywords: computer modelling; iPSC-CMs; variability.
© 2019 The Authors. The Journal of Physiology published by John Wiley & Sons Ltd on behalf of The Physiological Society.
Figures







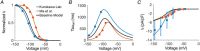







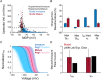
Comment in
-
To their own beat: modelling variability in induced pluripotent stem cell-derived cardiomyocytes.J Physiol. 2019 Oct;597(20):5047-5048. doi: 10.1113/JP278739. Epub 2019 Sep 30. J Physiol. 2019. PMID: 31441052 No abstract available.
References
-
- Bers DM (2000). Calcium fluxes involved in control of cardiac myocyte contraction. Circ Res 87, 275–281. - PubMed

