Hierarchical spherical deformation for cortical surface registration
- PMID: 31280090
- PMCID: PMC6733638
- DOI: 10.1016/j.media.2019.06.013
Hierarchical spherical deformation for cortical surface registration
Abstract
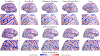
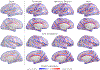
We present hierarchical spherical deformation for a group-wise shape correspondence to address template selection bias and to minimize registration distortion. In this work, we aim at a continuous and smooth deformation field to guide accurate cortical surface registration. In conventional spherical registration methods, a global rigid alignment and local deformation are independently performed. Motivated by the composition of precession and intrinsic rotation, we simultaneously optimize global rigid rotation and non-rigid local deformation by utilizing spherical harmonics interpolation of local composite rotations in a single framework. To this end, we indirectly encode local displacements by such local composite rotations as functions of spherical locations. Furthermore, we introduce an additional regularization term to the spherical deformation, which maximizes its rigidity while reducing registration distortion. To improve surface registration performance, we employ the second order approximation of the energy function that enables fast convergence of the optimization. In the experiments, we validate our method on healthy normal subjects with manual cortical surface parcellation in registration accuracy and distortion. We show an improved shape correspondence with high accuracy in cortical surface parcellation and significantly low registration distortion in surface area and edge length. In addition to validation, we discuss parameter tuning, optimization, and implementation design with potential acceleration.
Keywords: Cortical surface registration; Shape correspondence; Spherical deformation; Spherical harmonics.
Copyright © 2019 Elsevier B.V. All rights reserved.
Conflict of interest statement
Declaration of Competing Interest
The authors declare no conflict of interest.
Figures





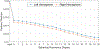





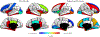

References
-
- Agrawal P, Whitaker RT, Elhabian SY, 2017. Learning deep features for automated placement of correspondence points on ensembles of complex shapes In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 185–193.
-
- Armstrong E, Schleicher A, Omran H, Curtis M, Zilles K, 1995. The ontogeny of human gyrification. Cerebral Cortex 5 (1), 56–63. - PubMed
-
- Auzias G, Lefèvre J, Le Troter A, Fischer C, Perrot M, Régis J, Coulon O, 2013. Model-driven harmonic parameterization of the cortical surface: Hip-hop. IEEE transactions on medical imaging 32 (5), 873–887. - PubMed
-
- Benjamini Y, Hochberg Y, 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the royal statistical society. Series B (Methodological), 289–300.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

