Estimation and prediction for a mechanistic model of measles transmission using particle filtering and maximum likelihood estimation
- PMID: 31290184
- PMCID: PMC6771900
- DOI: 10.1002/sim.8290
Estimation and prediction for a mechanistic model of measles transmission using particle filtering and maximum likelihood estimation
Abstract
Disease incidence reported directly within health systems frequently reflects a partial observation relative to the true incidence in the population. State-space models present a general framework for inferring both the dynamics of infectious disease processes and the unobserved burden of disease in the population. Here, we present a state-space model of measles transmission and vaccine-based interventions at the country-level and a particle filter-based estimation procedure. Our dynamic transmission model builds on previous work by incorporating population age-structure to allow explicit representation of age-targeted vaccine interventions. We illustrate the performance of estimators of model parameters and predictions of unobserved states on simulated data from two dynamic models: one on the annual time-scale of observations and one on the biweekly time-scale of the epidemiological dynamics. We show that our model results in approximately unbiased estimates of unobserved burden and the underreporting rate. We further illustrate the performance of the fitted model for prediction of future disease burden in the next one to 15 years.
Keywords: measles; particle filter; stochastic model; time series; under-reporting.
© 2019 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.
Conflict of interest statement
We report no conflicts of interest.
Figures
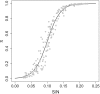
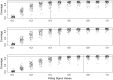
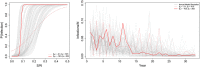
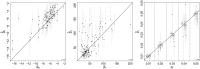
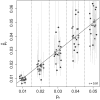
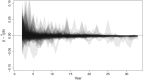

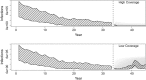
References
-
- Chen S, Fricks J, Ferrari MJ. Tracking measles infection through non‐linear state space models. J R Stat Soc Ser C Appl Stat. 2012;61(1):117‐134. 10.1111/j.1467-9876.2011.01001.x - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical
