Sticky collisions of ultracold RbCs molecules

Abstract

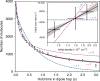
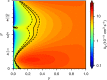
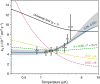
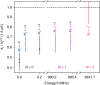
Understanding and controlling collisions is crucial to the burgeoning field of ultracold molecules. All experiments so far have observed fast loss of molecules from the trap. However, the dominant mechanism for collisional loss is not well understood when there are no allowed 2-body loss processes. Here we experimentally investigate collisional losses of nonreactive ultracold ⁸⁷Rb¹³³Cs molecules, and compare our findings with the sticky collision hypothesis that pairs of molecules form long-lived collision complexes. We demonstrate that loss of molecules occupying their rotational and hyperfine ground state is best described by second-order rate equations, consistent with the expectation for complex-mediated collisions, but that the rate is lower than the limit of universal loss. The loss is insensitive to magnetic field but increases for excited rotational states. We demonstrate that dipolar effects lead to significantly faster loss for an incoherent mixture of rotational states.

Fig. 1

Loss of ground state molecules. Collisional loss of molecules in $\mid N=0,M_N=0,m_i^{\mathrm{Rb}}=3\mathrm{∕}2,m_i^{\mathrm{Cs}}=7\mathrm{∕}2⟩$ with initial temperature of 1.5(1) μK and peak density 1.9(2) × 10¹¹ cm⁻³. Each result is the mean of at least five experimental runs, with standard error shown. The solid black line shows a fit to the coupled rate equations given in Eq. (2) with 1 standard deviation (σ) uncertainty in γ shaded. The dashed lines show fits to the data with fixed γ = 1, 2 and 3 corresponding to one-, two- and three-body loss, respectively. Inset: Density dependence of the initial loss rate on a log–log scale. The vertical error bars show the 1σ uncertainty in the linear gradient fitted to the first 200 ms of each loss measurement, and the horizontal error bars show the 1σ uncertainty in the density derived from the uncertainties in the starting temperature, number and trap frequencies. The solid line is a linear fit, with 1σ uncertainty in the gradient shaded, while the dashed lines indicate the expectations for one-, two- and three-body loss

Fig. 2

Thermally averaged loss rate coefficient from the single-channel model at 1.5 μK. k₂(T) is plotted as a function of the loss parameter y and the short-range phase shift δ^s. The solid and dashed black lines correspond to the measured k₂ and uncertainty, respectively

Fig. 3

Temperature dependence of the loss rate coefficient. The horizontal and vertical error bars show the 1σ uncertainties in the measured temperature and loss rate coefficient k₂, respectively. The coloured dashed lines all match the experimental rate coefficient at T = 1.5 μK, for a range of values labelled by y, δ^s that follow the solid black line in Fig. 2. The solid blue line shows the best fit, and the shaded region corresponds to the range of parameters that agree with the experimental results (open circles). The black line shows the loss rate in the universal limit (y = 1)

Fig. 4

Loss rates as a fraction of the universal limit in a range of rotational and hyperfine states. Molecules are prepared in a state (N, M_F) with T = 1.5(1) μK. The energy of each state is given relative to that of (0, +5). filled circles are measurements where the state is populated directly by STIRAP, whereas empty circles show where the molecules are transferred to the state with coherent microwave π-pulses (see methods). Error bars show the 1σ uncertainty in the measured rate constant k₂. Numerical values for the results are given in Supplementary Table 1