Universal quantized thermal conductance in graphene

Abstract

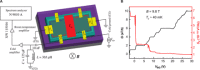
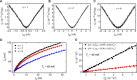
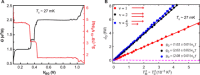
The universal quantization of thermal conductance provides information on a state's topological order. Recent measurements revealed that the observed value of thermal conductance of the $\frac{5}{2}$ state is inconsistent with either Pfaffian or anti-Pfaffian model, motivating several theoretical articles. Analysis has been made complicated by the presence of counter-propagating edge channels arising from edge reconstruction, an inevitable consequence of separating the dopant layer from the GaAs quantum well and the resulting soft confining potential. Here, we measured thermal conductance in graphene with atomically sharp confining potential by using sensitive noise thermometry on hexagonal boron-nitride encapsulated graphene devices, gated by either SiO₂/Si or graphite back gate. We find the quantization of thermal conductance within 5% accuracy for ν = $1;\frac{4}{3};2$ and 6 plateaus, emphasizing the universality of flow of information. These graphene quantum Hall thermal transport measurements will allow new insight into exotic systems like even-denominator quantum Hall fractions in graphene.

Fig. 1. Device configuration and QH response.

(A) Schematic of the device with measurement setup. The device is set in integer QH regime at filling factor ν = 1, where one chiral edge channel (line with arrow) propagates along the edge of the sample. The current I_SD is injected (green line) through the contact S, which is absorbed in the floating reservoir (red contact). Chiral edge channel (red line) at potential V_M and temperature T_M leave the floating reservoir and terminate into two cold grounds (CGs). The cold edges (without any current) at temperature T₀ are shown by the blue lines. The resulting increase in the electron temperature T_M of the floating reservoir is determined from the measured excess thermal noise at contact D. A resonant (LC) circuit, situated at contact D, with resonance frequency f₀ = 758 kHz, filters the signal, which is amplified by the cascade of amplification chain (preamplifier placed at 4K plate and a room temperature amplifier). Last, the amplified signal is measured by a spectrum analyzer. (B) Hall conductance measured at the contact S using lock-in amplifier at B = 9.8 T (black line). Thermal noise (including the cold amplifier noise) measured as a function of V_BG at f₀ = 758 kHz (red line). The plateaus for ν = 1, 2, and 6 are visible in both measurements.

Fig. 2. Thermal conductance in integer QH.

Excess thermal noise S_I is measured as a function of source current I_SD at ν = 1 (A), 2 (B), and 6 (C). (D) The increased temperatures T_M of the floating reservoir are plotted (solid circles) as a function of dissipated power J_Q for ν = 1 (N = 2), 2 (N = 4), and 6 (N = 12), respectively, where N = 2ν is the total outgoing channels from the floating reservoir. (E) The λ = ΔJ_Q/(0.5κ₀) is plotted as a function of $T_{\mathrm{M}}^2$ for ΔN = 2 (between ν = 1 and 2) and ΔN = 8 (between ν = 2 and 6), respectively, in red and black solid circles, where ΔJ_Q = J_Q(ν_i, T_M) − J_Q(ν_j, T_M). The solid lines are the linear fittings to extract the thermal conductance values. Slope of these linear fits are 1.92 and 7.92 for ΔN = 2 and 8, respectively, which gives the g_Q = 0.96κ₀T and 0.99κ₀T for the single edge mode, respectively.

Fig. 3. Thermal conductance in fractional QH.

(A) Hall conductance (black line) and thermal noise (red line) measured in the graphite back-gated device plotted as a function of V_BG at B = 7 T. The plateaus for ν = 1, $\frac{4}{3}$, and 2 are visible in both the measurements. (B) Similar to the previous plots (Fig. 2), the excess thermal noise S_I is measured as a function source current I_SD, and the T_M is shown as a function of the dissipated power J_Q in figs. S15 and S16, from which we have extracted the J_Q (solid circles) as a function of $T_{\mathrm{M}}^2-T_0^2$ for ν = 1, $\frac{4}{3}$, and 2 and shown up to T_M ~ 60 to 70 mK. The solid lines are the linear fits to extract the slopes, which give the thermal conductance values of 1.02, 2.08, and 2.02κ₀T for ν = 1, $\frac{4}{3}$, and 2, respectively. One can see that the thermal conductance values are quantized for ν = 1 and 2, and the values are the same for both the ν = $\frac{4}{3}$ and 2 plateaus. The inset shows the corresponding downstream charge modes for integer and fractional edges. The dashed curve represents the theoretically predicted (section S10) contribution of the heat Coulomb blockade (39, 40) for ν = 1, showing its negligible contribution to the net thermal current.