Intrinsically motivated collective motion

Abstract

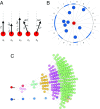
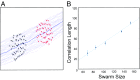
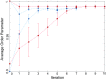
Collective motion is found in various animal systems, active suspensions, and robotic or virtual agents. This is often understood by using high-level models that directly encode selected empirical features, such as coalignment and cohesion. Can these features be shown to emerge from an underlying, low-level principle? We find that they emerge naturally under future state maximization (FSM). Here, agents perceive a visual representation of the world around them, such as might be recorded on a simple retina, and then move to maximize the number of different visual environments that they expect to be able to access in the future. Such a control principle may confer evolutionary fitness in an uncertain world by enabling agents to deal with a wide variety of future scenarios. The collective dynamics that spontaneously emerge under FSM resemble animal systems in several qualitative aspects, including cohesion, coalignment, and collision suppression, none of which are explicitly encoded in the model. A multilayered neural network trained on simulated trajectories is shown to represent a heuristic mimicking FSM. Similar levels of reasoning would seem to be accessible under animal cognition, demonstrating a possible route to the emergence of collective motion in social animals directly from the control principle underlying FSM. Such models may also be good candidates for encoding into possible future realizations of artificial "intelligent" matter, able to sense light, process information, and move.

Keywords: active matter; collective motion; intelligent matter.

Fig. 1.

Sketch showing an agent’s movement options, a representation of the visual state of the world around it, and its future decision tree. (A) The five actions available to each agent at every time step, given that its previous move was in the direction of the dashed line, continue in the same direction at a nominal/slow/fast speed or turn left/right, respectively. (B) A representative agent (red) sees the other agents (blue) geometrically projected onto a retina-like sensor array. Each sensor registers 1 if a line of sight through more than half of its angular region intersects other disk(s), corresponding to the solid blue regions on the perimeter; 0 otherwise. This $n_s$-dimensional Boolean vector is the agent’s sensory input and represents its “state.” Here, we show $n_s=20$, for clarity. (C) The spatial positions that an agent, shown as red, can access in the future form nodes on a fan-like tree, color-coded by the time into the future: pink/red (one step), cyan (two steps), orange (three steps), magenta (four steps), and green (five steps); in this cartoon, the maximum future time horizon is therefore $\tau =5$. The branch of this tree that the agent explores is contingent on its next move (here shown as a turn to the left, in red). A similar branch exists for the four other possible moves, but these are omitted for clarity. The red agent computes the future sensory states accessible to it at each future node, as described in B, choosing the move in the next time step that leads to the branch with the largest number of distinct visual states. The nodes that are highlighted in dotted red correspond to positions that the agent anticipates will overlap (“collide”) with other agents. Here, a single other colliding agent is shown in blue, for clarity. When computing the number of distinct visual states, we exclude those from nodes that correspond to, or follow after, such a collision.

Fig. 2.

(A) Structure of collective swarms that emerge under FSM dynamics, as described in Fig. 1A. Shown are snapshots of a typical realization at two different times showing the trajectories of the agents (light dashed lines) and center of mass (dark dotted line), with $N=50$, $n_s=40$, $v_0=10$, $\mathrm{\Delta }v=2$, and $\mathrm{\Delta }\theta =15^{○}$ and a time-horizon of $\tau =4$. Wedges show agents’ direction of motion; Movie S1. (B) The center-of-mass frame velocity correlation function for agents is computed for systems with the same parameter values, except that the data points correspond to $N=\mathrm{50,\; 75,\; 100,\; 150,\; 200}$ agents. Shown is the correlation length thereby obtained, here defined as the distance at which this correlation function crosses zero (nearby agents are positively correlated; distant ones are negatively correlated). This correlation length is compared against the corresponding swarm size, with the square root of the area of a convex hull containing all agents. See SI Appendix for details.

Fig. 3.

Snapshots of a swarm made up of $N=500$ agents with $\tau =5$, shown at different times in a frame comoving with the swarm’s center of mass. A shows the initial state of the swarm, and then B–D show snapshots of its subsequent evolution (in chronological order). In this example, we use a continuous measure of visual degeneracy (see SI Appendix for details). The full simulation is shown in Movie S4.

Fig. 4.

Convergence of heuristics A (order targeting; blue) and B [topological Vicsek (5); red] to a value of the order parameter that is self-consistent with the value realized by FSM in each case. An initial (iteration 0) order parameter for the heuristic (${\varphi }_A\hspace{0.17em}\mathrm{\text{and}}\hspace{0.17em}{\varphi }_B,\mathrm{\text{respectively}}$) is chosen. This parameterizes the model of all (other) agents to be used when constructing their trajectories into the future to apply FSM on each agent’s predicted future visual states. The average order realized by the FSM simulation then serves as the order parameter for the heuristic in the next iteration, and the process is repeated. The order converges, both from above and below, to an average order parameter that is the same, both for the heuristic and the motion generated by FSM using that heuristic to model the behavior of other agents. FSM under heuristic A is unstable for values of ${\varphi }_A\lesssim 0.9$, leading to flock fragmentation into (ordered) subgroups. Parameter values are as given in Fig. 2. See also Movie S5.

Fig. 5.

Training a neural network as a heuristic approximating FSM. (A) Sketch of the network architecture. The network takes as its input the agent’s current speed and the state of each sensor in both the current and previous time steps, represented as light and dark blue squares on each sensor (left-hand side). This is then passed through four hidden layers of neurons of sizes 200; 100; 50; and 25, which have RelU activation functions. These are attached to a softmax classifier which outputs an integer between 1 and 5, identifying the next move (final output; right-hand side). The network was trained to mimic FSM trajectories using 10 million examples (data from 200,000 simulation time steps). (B) The output dynamics from this network is seen to closely mimic the FSM trajectories shown in Fig. 2; Movie S6.