Divide-and-conquer strategy for large-scale Eulerian solvent excluded surface

Abstract

Motivation: Surface generation and visualization are some of the most important tasks in biomolecular modeling and computation. Eulerian solvent excluded surface (ESES) software provides analytical solvent excluded surface (SES) in the Cartesian grid, which is necessary for simulating many biomolecular electrostatic and ion channel models. However, large biomolecules and/or fine grid resolutions give rise to excessively large memory requirements in ESES construction. We introduce an out-of-core and parallel algorithm to improve the ESES software.

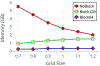
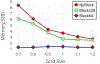
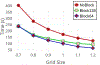
Results: The present approach drastically improves the spatial and temporal efficiency of ESES. The memory footprint and time complexity are analyzed and empirically verified through extensive tests with a large collection of biomolecule examples. Our results show that our algorithm can successfully reduce memory footprint through a straightforward divide-and-conquer strategy to perform the calculation of arbitrarily large proteins on a typical commodity personal computer. On multi-core computers or clusters, our algorithm can reduce the execution time by parallelizing most of the calculation as disjoint subproblems. Various comparisons with the state-of-the-art Cartesian grid based SES calculation were done to validate the present method and show the improved efficiency. This approach makes ESES a robust software for the construction of analytical solvent excluded surfaces.

Availability and implementation: http://weilab.math.msu.edu/ESES.

Figure 1:. Illustration of subdomain based algorithm.

The bounding box of the whole molecular surface is divided into several non-overlapping subdomains, which can be computed independently with a small memory footprint. Finally, patches of the SES from each subdomain can be assembled into a watertight surface identical to the one constructed with ESES. Note that the patches form a watertight surface, the gaps between the adjacent patches from different subdomains are added for visualization only.

Figure 2:. 2D Index mapping Example.

All the indices are 0-based. Given a cell with global coordinates (i, j) in block (k, l) (green) and its local coordinates (m, n) within the block, the one-to-one mapping is straightforward as illustrated. Note that (m, n) would require fewer bits to store than (i, j). This is typical in parallel processing such as CUDA threads.

Figure 3:. Redundancy elimination.

For each subdomain, we only keep the information on faces with a normal along negative axis directions (red), the other faces (yellow) are omitted because they have already been accounted for by adjacent subdomains. After concatenation (dashed line), only the output for faces of the entire grid with normals along the positive axis directions is missing. However, with the margin padded to the molecule when constructing the domain, they do not contain any intersection information to begin with.

Figure 4:. Illustration of the SES generation of multiprotein complex.

Here we show the assembly of 3j2u proteins with different chains being marked by different colors. Inner ring: microtubule; intermediate ring: kinesin-13 head domain; and outer ring: curved tubulin protofilament.

Figure 5:. Illustration of the building block protein 3j2u.

It shows Drosophila melanogaster kinesin-13 head domain (yellow) binding to tubulin protofilament (silver and blue) and microtubule (red and green).

Figure 6:

Two models, proteins 5z10 (left) and 5vkq (right), on which tests and statistics of the present algorithm are performed.

Figure 7:. Memory footprint comparison at various grid spacings (Å) for protein 5z10 (single-thread).

Curves with circular, square and diamond nodes are corresponding to no block assigned, block size 128 assignment, and block size 64 assignment, respectively.

Figure 8:. Execution time comparison at various grid spacings (Å) for protein 5z10 (single-thread).

Curves with circular, square and diamond nodes are corresponding to no block assigned, block size 128 assignment, and block size 64 assignment, respectively.

Figure 9:. Memory footprint comparison at various grid spacings (Å) for protein 5vkq (8-threads).

Curves with circular, square and diamond nodes are corresponding to no block assigned, block size 128 assignment, and block size 64 assignment, respectively.

Figure 10:. Execution time comparison at various grid spacings (Å) for protein 5vkq (8-threads).

Curves with circular, square and diamond nodes are corresponding to no block assigned, block size 128 assignment, and block size 64 assignment, respectively.

Figure 11:. Execution time analysis.

The scatter plot of execution time vs the number of atoms is given for 290 proteins when 8 threads are used.