Bayesian inference of distributed time delay in transcriptional and translational regulation

Abstract

Motivation: Advances in experimental and imaging techniques have allowed for unprecedented insights into the dynamical processes within individual cells. However, many facets of intracellular dynamics remain hidden, or can be measured only indirectly. This makes it challenging to reconstruct the regulatory networks that govern the biochemical processes underlying various cell functions. Current estimation techniques for inferring reaction rates frequently rely on marginalization over unobserved processes and states. Even in simple systems this approach can be computationally challenging, and can lead to large uncertainties and lack of robustness in parameter estimates. Therefore we will require alternative approaches to efficiently uncover the interactions in complex biochemical networks.

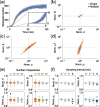
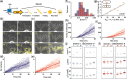
Results: We propose a Bayesian inference framework based on replacing uninteresting or unobserved reactions with time delays. Although the resulting models are non-Markovian, recent results on stochastic systems with random delays allow us to rigorously obtain expressions for the likelihoods of model parameters. In turn, this allows us to extend MCMC methods to efficiently estimate reaction rates, and delay distribution parameters, from single-cell assays. We illustrate the advantages, and potential pitfalls, of the approach using a birth-death model with both synthetic and experimental data, and show that we can robustly infer model parameters using a relatively small number of measurements. We demonstrate how to do so even when only the relative molecule count within the cell is measured, as in the case of fluorescence microscopy.

Availability and implementation: Accompanying code in R is available at https://github.com/cbskust/DDE_BD.

Supplementary information: Supplementary data are available at Bioinformatics online.

Fig. 1.

Estimation of the delay distributions using multiple trajectories is accurate and precise. (a) Simulated trajectories of a delayed stochastic birth–death process (Eq. 5) with rate parameters A = 30 min^–1, B = 0.05 min^–1 and delay $\tau \sim \Gamma (18/5,3/5)$, i.e. ${\mu }_{\tau }=6$ min and ${\sigma }_{\tau }^2=10$ min². We assumed that $X(0)=0$. Trajectories used for inference were sampled at 1 min intervals. (b–d) MCMC generated samples from the posterior distributions over parameters using a single trajectory (orange) or 40 trajectories (blue). While the rate parameters, A, B, can be estimated well using a single trajectory (b), estimation of the delay $\tau \sim \Gamma (\alpha ,\beta )$ requires multiple trajectories (c and d). Here, the sample values were normalized by dividing with the true parameter values. (e) Box plots of 100 posterior means using an increasing number of trajectories. Subsets of between 5 and 40 trajectories were chosen randomly and repeatedly from a set of 500 simulations. Estimates were normalized by dividing by the true parameter values. (f) Increased sampling rate leads to more accurate estimation. Note that sparser measurements, at intervals of 2 and 6 min, still allowed for reasonably accurate and precise estimates of all parameters, as long as a sufficient number of trajectories was used (40 in this case). (Color version of this figure is available at Bioinformatics online.)

Fig. 2.

The mean, but not the variance of the delay can be accurately and precisely estimated when the delay distribution is misspecified. (a) Three types of delay distributions: $\Gamma (18/5,3/5)$, Inverse-$\Gamma (28/5,138/5)$ and $12·B(1.3,1.3)$. For all distributions ${\mu }_{\tau }=6,$ and ${\sigma }_{\tau }^2=10$. (b) A box plot of 100 posterior mean estimates. As in Fig. 1, parameters were estimated using 40 sample trajectories randomly and repeatedly chosen from a set of 500 trajectories generated assuming one of the three delay distributions shown in panel (a). Here the estimates were normalized by dividing with their true values

Fig. 3.

Measurements of dilution rate allow for accurate estimation when only relative molecular levels measurements are available. (a) The average (dashed) and variance (solid) of the 500 simulated trajectories in Figure 1a, scaled by 0.5, 1 and 2. The average and variance of the scaled trajectories were scaled by different amounts (blue and green). (b) Using scaled trajectories to estimate delays leads to large biases. Here, we show box plots based of 100 posterior means, each estimated using 40 subsampled trajectories. (c) When the dilution rate, B, is known, the delay distribution can be accurately and precisely estimated even with incorrectly scaled data. (Color version of this figure is available at Bioinformatics online.)

Fig. 4.

Robust estimation of the time delay distribution of YFP synthesis after induction. (a) When ARA is added to the media, AraC promotes the synthesis of YFP. The synthesis process involves transcription, translation, protein folding and maturation which result in a delay between YFP gene activation, and the observation of the fluorescence signal generated by mature YFP. (b, c) Time-lapse images of YFP expression from two independent experiments, performed previously (Cheng et al., 2017). At 12 min after measurement was started, 2% ARA was added to the media, promoting the constitutive transcription of YFP. (d, e) The lineage of each cell was identified via manual segmentation of images, and the change in individual cell areas was tracked [39 cells in (d) and 29 cells in (e)]. When a mother cell divided into two daughter cells, the area of the mother cell was added to the area of the daughter cell. (f) We estimated dilution rates by fitting an exponential function to the cell growth data. The average dilution rate of the 39 cells from the first, and the 29 cells from the second experiment are 0.015 ± 0.005 and 0.016 ± 0.005 min^–1, respectively. (g) A conversion constant from YFP signal level to the number of YFP molecules (γ) was estimated by measuring the binomial error in partition of total YFP signal ($Y_{\text{tot}}$) at cell division to two daughter cells (Y₁ and Y₂). The constant γ was estimated as described in the text. (h, i) We estimated YFP molecule number per unit area by dividing the total fluorescence level of each individual cell (b, c) with its total area (d, e), and with the estimated scaling factor γ (g). (j–m) Using our inference algorithm with these trajectories, and fixing the dilution rate at the estimated value, B = 0.015, we obtained 10⁴ posterior samples for the remaining parameters (j, l). Due to the higher molecular numbers in (h) than (i), the estimated birth rate, A and delay variance, ${\sigma }_{\tau }^2,$ were higher and lower, respectively, in (j) than (l): 35.4 ± 0.4 and 23.1 ± 0.5, and 7.4 ± 0.7 and 13.4 ± 1.4. However, the estimated mean delay time, ${\mu }_{\tau },$ was similar in the two cases: 6.6 ± 0.1 min (j) and 7.5 ± 0.2 min (l). Estimation of the delay mean and variance was robust to the twofold change in γ (j and l) and B (k and m)