Strong magnetophonon oscillations in extra-large graphene

Abstract

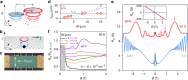
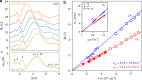
Van der Waals materials and their heterostructures offer a versatile platform for studying a variety of quantum transport phenomena due to their unique crystalline properties and the exceptional ability in tuning their electronic spectrum. However, most experiments are limited to devices that have lateral dimensions of only a few micrometres. Here, we perform magnetotransport measurements on graphene/hexagonal boron-nitride Hall bars and show that wider devices reveal additional quantum effects. In devices wider than ten micrometres we observe distinct magnetoresistance oscillations that are caused by resonant scattering of Landau-quantised Dirac electrons by acoustic phonons in graphene. The study allows us to accurately determine graphene's low energy phonon dispersion curves and shows that transverse acoustic modes cause most of phonon scattering. Our work highlights the crucial importance of device width when probing quantum effects and also demonstrates a precise, spectroscopic method for studying electron-phonon interactions in van der Waals heterostructures.

Fig. 1

Size-dependent magnetoresistance oscillations in mesoscopic graphene devices. a Landau level spectra of graphene. The diagram illustrates a carrier with momentum k₁ (black sphere) making a transition between Landau levels (blue and red rings) by resonant absorption of a phonon (brown arrow) with momentum q = |k₁−k₂| and energy ħω_q. Solid black arrows represent the magnitudes of wave vectors k₁, k₂ and q. b The semiclassical motion of a carrier (black sphere) in real space for the resonance condition sketched in a. The red and blue circles which touch at a tangent point represent the initial and final semiclassical cyclotron orbits of two Landau-quantised states between which an electron is scattered by a phonon. During resonant scattering, the carriers follow a path that resembles the number 8 (figure of eight trajectory). The red and blue arrows show the motion of the charge carriers along this trajectory. The green arrow indicates direction of the applied current I. c Optical image of a graphene device with W = 15 μm. The edges of the mesa are indicated by the white solid line. d Open circles plot experimentally determined Drude mean free path L_MFP as a function of W for two T and fixed n = −2 × 10¹²cm⁻². Black dashed line plots the equation L_MFP = W. Solid green line marks the phonon-limited mean free path (L_e–ph) at 50 K. Our measurements focussed on the valence band because our wide devices exhibited higher electronic quality for hole doping (e), longitudinal magnetoresistance data R_xx (B) for fixed n = −3.3 × 10¹²cm⁻² measured in our wide device (c) at two different T. The red arrows indicate peaks that are caused by magnetophonon resonance (MPR). The 50 K curve is off-set vertically for clarity. Inset: Hall resistance R_xy(B) measured simultaneously as R_xx. The solid blue and dashed red lines are data measured at 5 and 50 K respectively. f R_xx/R_{xx (B = 0T)} measured at fixed n and T in several devices of different W. The shaded area close to B = 0 contains semiclassical effects

Fig. 2

Temperature dependence of the magnetophonon effect. a Magnetoresistance R_xx (B) for T between 5 K (blue curve) and 100 K (black curve) in 5 K steps for fixed n measured in another Hall bar with W = 15 μm. b Extended data set of a showing high T behaviour (10 K steps). c Temperature dependence of the amplitude of MPR peaks, ΔR_xx (T), indicated in a by colour coded letters, p = 1–5

Fig. 3

Density dependence of magnetophonon oscillations. a Longitudinal resistance R_xx (grey scale map) as a function of n and B measured at 5 K (W = 15 μm). Logarithmic grey scale: white: 1 Ω to black: 15 Ω. The blue dashed lines trace Landau gaps corresponding to high filling factors ν = nh/Be. b Same as a measured at 50 K. Logarithmic grey scale: white: 5.5 Ω to black: 18 Ω. The red dashed lines plot Eq. (1) for p = 1 to 4 which corresponds to carriers scattering with transitions across 1 to 4 Landau level spacings. Features appearing for B < 0.2 T are the semiclassical geometrical oscillations not relevant in this work (see Supplementary Note 2 for details)

Fig. 4

Phonon spectroscopy in graphene by measurement of magnetophonon oscillations. a Longitudinal resistance R_xx as a function of B measured for several high n of holes in our wide (W = 13.8 μm) dual-gated graphene Hall bar. The curves have been off-set vertically for clarity. b Red symbols plot the fundamental frequency B_F ≡ pB_p of magnetophonon oscillations as a function of absolute n for three different devices; open circles correspond to the dual-gated device which allowed high doping. The blue symbols mark the positions B_p=1 of the broad peak (indicated by coloured arrows in a) which appears clearly at high n. The red and blue solid lines represents Eq. (1) with v_s/v_F = 0.0128 and 0.0198 respectively. Knowing v_F (Supplementary Note 5) we extract the TA (v_TA) and LA (v_LA) phonon velocities. Inset: Data in main panel transformed to phonon dispersion curves. Coloured squares−experimental data points (error bars reflect the error in the experimentally extracted v_F), solid lines plot the equation ħω_q = ħv_sq (same v_s as in the main panel), purple stars—data taken from ref. . c Calculation of the oscillatory part of the resistivity Δρ_xx(Ω) using the Kubo formula (see Supplementary Note 6 for details)