Biomarkers for Aging Identified in Cross-sectional Studies Tend to Be Non-causative
- PMID: 31353411
- PMCID: PMC7457180
- DOI: 10.1093/gerona/glz174
Biomarkers for Aging Identified in Cross-sectional Studies Tend to Be Non-causative
Abstract
Biomarkers are important tools for diagnosis, prognosis, and identification of the causal factors of physiological conditions. Biomarkers are typically identified by correlating biological measurements with the status of a condition in a sample of subjects. Cross-sectional studies sample subjects at a single timepoint, whereas longitudinal studies follow a cohort through time. Identifying biomarkers of aging is subject to unique challenges. Individuals who age faster have intrinsically higher mortality rates and so are preferentially lost over time, in a phenomenon known as cohort selection. In this article, we use simulations to show that cohort selection biases cross-sectional analysis away from identifying causal loci of aging, to the point where cross-sectional studies are less likely to identify loci that cause aging than if loci had been chosen at random. We go on to show this bias can be corrected by incorporating correlates of mortality identified from longitudinal studies, allowing cross-sectional studies to effectively identify the causal factors of aging.
Keywords: Epigenetics; Gerontology; Longevity; Mortality; Senescence.
© The Author(s) 2019. Published by Oxford University Press on behalf of The Gerontological Society of America. All rights reserved. For permissions, please e-mail: journals.permissions@oup.com.
Figures
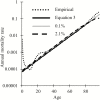
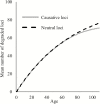

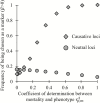

References
-
- Medawar PB. An Unsolved Problem of Biology: An Inaugural Lecture Delivered at University College, London. London: H.K. Lewis & Co; 1952.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

