Robustness of respiratory rhythm generation across dynamic regimes
- PMID: 31361738
- PMCID: PMC6697358
- DOI: 10.1371/journal.pcbi.1006860
Robustness of respiratory rhythm generation across dynamic regimes
Abstract
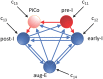
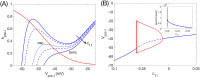
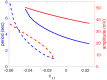
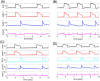
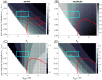
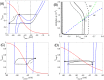
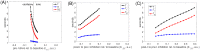
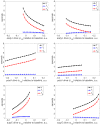
A central issue in the study of the neural generation of respiratory rhythms is the role of the intrinsic pacemaking capabilities that some respiratory neurons exhibit. The debate on this issue has occurred in parallel to investigations of interactions among respiratory network neurons and how these contribute to respiratory behavior. In this computational study, we demonstrate how these two issues are inextricably linked. We use simulations and dynamical systems analysis to show that once a conditional respiratory pacemaker, which can be tuned across oscillatory and non-oscillatory dynamic regimes in isolation, is embedded into a respiratory network, its dynamics become masked: the network exhibits similar dynamical properties regardless of the conditional pacemaker node's tuning, and that node's outputs are dominated by network influences. Furthermore, the outputs of the respiratory central pattern generator as a whole are invariant to these changes of dynamical properties, which ensures flexible and robust performance over a wide dynamic range.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

Similar articles
-
Modeling neural mechanisms for genesis of respiratory rhythm and pattern. II. Network models of the central respiratory pattern generator.J Neurophysiol. 1997 Apr;77(4):2007-26. doi: 10.1152/jn.1997.77.4.2007. J Neurophysiol. 1997. PMID: 9114251
-
Eupnea, tachypnea, and autoresuscitation in a closed-loop respiratory control model.J Neurophysiol. 2017 Oct 1;118(4):2194-2215. doi: 10.1152/jn.00170.2017. Epub 2017 Jul 19. J Neurophysiol. 2017. PMID: 28724778 Free PMC article.
-
Models of respiratory rhythm generation in the pre-Bötzinger complex. II. Populations Of coupled pacemaker neurons.J Neurophysiol. 1999 Jul;82(1):398-415. doi: 10.1152/jn.1999.82.1.398. J Neurophysiol. 1999. PMID: 10400967
-
Respiratory rhythm generation in neonatal and adult mammals: the hybrid pacemaker-network model.Respir Physiol. 2000 Sep;122(2-3):131-47. doi: 10.1016/s0034-5687(00)00155-9. Respir Physiol. 2000. PMID: 10967340 Review.
-
The Onset of the Fetal Respiratory Rhythm: An Emergent Property Triggered by Chemosensory Drive?Adv Exp Med Biol. 2017;1015:163-192. doi: 10.1007/978-3-319-62817-2_10. Adv Exp Med Biol. 2017. PMID: 29080027 Review.
Cited by
-
Cardiogenic and chronobiological mechanisms in seizure-induced sinus arrhythmias.PLoS Comput Biol. 2025 Jul 16;21(7):e1013318. doi: 10.1371/journal.pcbi.1013318. eCollection 2025 Jul. PLoS Comput Biol. 2025. PMID: 40668822 Free PMC article.
-
Asymmetric neuromodulation in the respiratory network contributes to rhythm and pattern generation.Front Neural Circuits. 2025 Jul 8;19:1532401. doi: 10.3389/fncir.2025.1532401. eCollection 2025. Front Neural Circuits. 2025. PMID: 40697628 Free PMC article.
-
Insights into the dynamic control of breathing revealed through cell-type-specific responses to substance P.Elife. 2019 Dec 5;8:e51350. doi: 10.7554/eLife.51350. Elife. 2019. PMID: 31804180 Free PMC article.
-
Predictions and experimental tests of a new biophysical model of the mammalian respiratory oscillator.Elife. 2022 Jul 7;11:e74762. doi: 10.7554/eLife.74762. Elife. 2022. PMID: 35796425 Free PMC article.
-
Asymmetric neuromodulation in the respiratory network contributes to rhythm and pattern generation.bioRxiv [Preprint]. 2024 Nov 11:2024.11.11.623076. doi: 10.1101/2024.11.11.623076. bioRxiv. 2024. Update in: Front Neural Circuits. 2025 Jul 08;19:1532401. doi: 10.3389/fncir.2025.1532401. PMID: 39605441 Free PMC article. Updated. Preprint.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

