Not all phylogenetic networks are leaf-reconstructible

Abstract

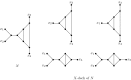
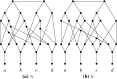
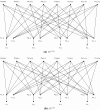
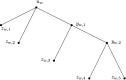
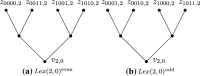
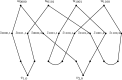
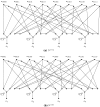
Unrooted phylogenetic networks are graphs used to represent reticulate evolutionary relationships. Accurately reconstructing such networks is of great relevance for evolutionary biology. It has recently been conjectured that all unrooted phylogenetic networks for at least five taxa can be uniquely reconstructed from their subnetworks obtained by deleting a single taxon. Here, we show that this conjecture is false, by presenting a counter-example for each possible number of taxa that is at least 4. Moreover, we show that the conjecture is still false when restricted to binary networks. This means that, even if we are able to reconstruct the unrooted evolutionary history of each proper subset of some taxon set, this still does not give us enough information to reconstruct their full unrooted evolutionary history.

Keywords: Graph reconstruction; Leaf removal; Phylogenetic Networks; Phylogenetics; Ulam’s Conjecture; Undirected graphs.

Fig. 1

Example of a phylogenetic network N and its X-deck

Fig. 2

The underlying undirected networks N and $N^{\prime }$ of two rooted networks which, in Huber et al. (2014), were shown to have the same induced subnetworks for any strict subset of the leaf set $X=\{a,b,c,d\}$. We observe that $N_d\nsim N_d^{\prime }$, since the shortest path between a and b has length 7 in $N_d$ and length 6 in $N_d^{\prime }$. Hence, these networks can not be used as counter-example for the leaf-reconstruction conjecture

Fig. 3

Non-binary example of $M^{\mathrm{even}}$ and $M^{\mathrm{odd}}$ for the case when when $r=4$. Vertices $u_w$ are adjacent to vertices $v_{i,h}$ if and only if $w_i=h$

Fig. 4

The caterpillar Cat(w) for the case $r=5$

Fig. 5

The lexicographic trees $Lex{(2,0)}^{\mathrm{even}}$ and $Lex{(2,0)}^{\mathrm{odd}}$ for the case $r=4$. Leaves of $Lex{(2,0)}^{\mathrm{even}}$ (respectively, $Lex{(2,0)}^{\mathrm{odd}}$) are $z_{w,2}$ for every length-r sequence w of even weight (odd weight) such that $w_2=0$

Fig. 6

A cycle containing the vertices $u_{0000},u_{0101},u_{1001},u_{1100}$ in $G^{\mathrm{even}}$ for the case $r=4$

Fig. 7

Binary example of $N^{\mathrm{even}}$ and $N^{\mathrm{odd}}$ for the case when when $r=4$. The vertex $u_{0000}$ in $N^{\mathrm{even}}$ has distance $d_1=3$ from $x_1$, $d_2=3$ from $x_2$, $d_3=4$ from $x_3$, and $d_4=4$ from $x_4$. Moreover there is no vertex in $N^{\mathrm{odd}}$ with distance $d_i$ from $x_i$ for each $i\in [4]$. Thus $N^{\mathrm{even}}$ and $N^{\mathrm{odd}}$ are not equivalent. However, for each $i\in [4]$ the multigraphs ${(N^{\mathrm{even}})}_{x_i}$ and ${(N^{\mathrm{odd}})}_{x_i}$ are equivalent, using an isomorphism that maps each vertex $u_w$ to $u_{w^{\nsim i}}$