Identifying important parameters in the inflammatory process with a mathematical model of immune cell influx and macrophage polarization

Abstract

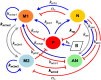
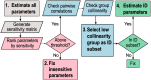
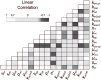
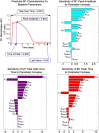
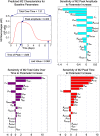
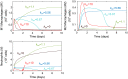
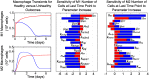
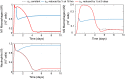
In an inflammatory setting, macrophages can be polarized to an inflammatory M1 phenotype or to an anti-inflammatory M2 phenotype, as well as existing on a spectrum between these two extremes. Dysfunction of this phenotypic switch can result in a population imbalance that leads to chronic wounds or disease due to unresolved inflammation. Therapeutic interventions that target macrophages have therefore been proposed and implemented in diseases that feature chronic inflammation such as diabetes mellitus and atherosclerosis. We have developed a model for the sequential influx of immune cells in the peritoneal cavity in response to a bacterial stimulus that includes macrophage polarization, with the simplifying assumption that macrophages can be classified as M1 or M2. With this model, we were able to reproduce the expected timing of sequential influx of immune cells and mediators in a general inflammatory setting. We then fit this model to in vivo experimental data obtained from a mouse peritonitis model of inflammation, which is widely used to evaluate endogenous processes in response to an inflammatory stimulus. Model robustness is explored with local structural and practical identifiability of the proposed model a posteriori. Additionally, we perform sensitivity analysis that identifies the population of apoptotic neutrophils as a key driver of the inflammatory process. Finally, we simulate a selection of proposed therapies including points of intervention in the case of delayed neutrophil apoptosis, which our model predicts will result in a sustained inflammatory response. Our model can therefore provide hypothesis testing for therapeutic interventions that target macrophage phenotype and predict outcomes to be validated by subsequent experimentation.

Fig 1. Experimental details.

Gating strategy and representative dot plots and histograms used to identify individual cell populations.

Fig 2. Model schematic.

Model schematic for the inflammatory response with variables defined in the equations. Arrows represent up-regulation and bars represent destruction or inhibition. Parameters in the schematic that are included in the final subset of identifiable parameters appear in bold; additional non-interaction parameters that do not appear in the schematic are given with the full subset in Table 4.

Fig 3. Steps to estimate an identifiable subset of parameters.

Step 1 (gray): estimate all parameters and generate a discretized sensitivity matrix from the fitted model. Step 2 (pink): Fix parameters that fall below a determined sensitivity threshold. Step 3 (blue): Select one group of low collinearity (identifiable) parameters. Step 4 (green): Estimate the chosen identifiable subset and fix all other parameters.

Fig 4. Parameter importance ranking (RMS) for full and identifiable model.

We ranked the impact of each parameter on all three observable model outputs (N, M1, and M2) by calculating a root mean square sensitivity measure, as defined in Brun et al. [34]. The sensitivity threshold was set at 5% of the maximum RMS value calculated over all parameters. Eight parameters in the full model were thus deemed insensitive and fixed in step 2 of our identifiability analysis. The inset plot shows RMS values for the identifiable model.

Fig 5. Correlation matrix plot for the full model.

An approximate correlation matrix was obtained from the Fisher Information Matrix for the sensitive subset of parameters and used to visualize correlations. There are many significant linear correlations (greater than 0.7) between sensitive parameters that appear as black or white squares on the off diagonal.

Fig 6. Model predictions for the identifiable model.

Model response variable predictions for M1 macrophage (M1), M2 macrophage (M2), and neutrophil (N) counts are plotted versus mean observed values and standard errors. Model state variable predictions for levels of pathogen (P) and nutrient (B) and apoptotic neutrophil (AN) counts are plotted on the same axis. The blue axis applies to pathogen and apoptotic neutrophils. The red axis applies to nutrient broth.

Fig 7. Baseline characteristics for M1 and sensitivity of characteristics to parameter variations.

The M1 transient curve and its characteristics are plotted for the baseline parameter values given in Tables 1 and 4. Parameter sensitivity plots show the effects on M1 characteristics of varying model parameters one-at-a-time by a factor of 1.001 of its baseline value while holding all other parameters at their baseline values. Insensitive parameters, which have zero sensitivity for all characteristics, are not shown.

Fig 8. Baseline characteristics for M2 and sensitivity of characteristics to parameter variations.

The M2 transient curve and its characteristics are plotted for baseline parameter values given in Tables 1 and 4. Parameter sensitivity plots show the effects on M2 characteristics of varying model parameters one-at-a-time by a factor of 1.001 of its baseline value while holding all other parameters at their baseline values. Insensitive parameters, which have zero sensitivity for all characteristics, are not shown.

Fig 9. Results of perturbations in parameter k_an.

Parameter k_an, which models the rate of neutrophil apoptosis, was varied around its baseline value of k_an = 7.108. The effects of variations on M1, M2, and neutrophils are shown. Values lower than baseline lead to a sustained inflammatory response from all immune cells while higher values shorten the time course of each.

Fig 10. Sensitivity of M1 and M2 characteristics to parameter variations in the case of delayed neutrophil apoptosis (unhealthy response) versus a healthy response.

Predictions and sensitivities for a healthy response are plotted in blue, while predictions and sensitivities for an unhealthy response are plotted in red. A healthy M1 and M2 response that resolves, with all parameters at baseline values given in Tables 1 and 4 (including k_an = 7.108), is plotted versus an unhealthy, sustained M1 and M2 response resulting from reducing the value of parameter k_an to 5.56 while holding all other parameters constant. The bar charts compare the associated sensitivity of M1 and M2 characteristics to parameter variations in the healthy case versus the unhealthy case. Insensitive parameters, which have zero sensitivity for all characteristics, are not shown.

Fig 11. Parameter variations that resolve inflammation in the case of delayed neutrophil apoptosis.

Reducing the value of parameter k_an from baseline while holding all other parameters constant leads to sustained inflammation. We resolved inflammation in this case by varying each of three parameters separately: μ_m2, u_nr, or s_nr. All immune cells return to low levels if resting neutrophil influx or decay is modulated, while a population of M2 macrophages persists if M2s are directly targeted to resolve the inflammation.

Fig 12. Predicted effects of reducing source of monocytes s_mr.

The effects of the baseline case of a constant influx of resting monocytes (that will differentiate into macrophages) is compared to the effects of reducing influx of monocytes at an early timepoint (16 hours) versus a late timepoint (5 days). Early intervention leads to sustained inflammation while late intervention leads to an increase in neutrophils.