Robust Optimal Design of Energy Efficient Series Elastic Actuators: Application to a Powered Prosthetic Ankle
- PMID: 31374719
- PMCID: PMC6684305
- DOI: 10.1109/ICORR.2019.8779446
Robust Optimal Design of Energy Efficient Series Elastic Actuators: Application to a Powered Prosthetic Ankle
Abstract
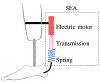
Design of rehabilitation and physical assistance robots that work safely and efficiently despite uncertain operational conditions remains an important challenge. Current methods for the design of energy efficient series elastic actuators use an optimization formulation that typically assumes known operational requirements. This approach could lead to actuators that cannot satisfy elongation, speed, or torque requirements when the operation deviates from nominal conditions. Addressing this gap, we propose a convex optimization formulation to design the stiffness of series elastic actuators to minimize energy consumption and satisfy actuator constraints despite uncertainty due to manufacturing of the spring, unmodeled dynamics, efficiency of the transmission, and the kinematics and kinetics of the load. To achieve convexity, we write energy consumption as a scalar convex-quadratic function of compliance. As actuator constraints, we consider peak motor torque, peak motor velocity, limitations due to the speed-torque relationship of DC motors, and peak elongation of the spring. We apply our formulation to the robust design of a series elastic actuator for a powered prosthetic ankle. Our simulation results indicate that a small trade-off between energy efficiency and robustness is justified to design actuators that can operate with uncertainty.
Figures

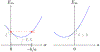


References
-
- Pratt G and Williamson M, “Series Elastic Actuators,” in Proc. IEEE/RSJ Int. Conf. Intell. Robot. Syst. Hum. Robot Interact. Coop. Robot., vol. 1 IEEE Comput. Soc. Press, 1995, pp. 399–406.
-
- Hogan N, “Impedance Control: An Approach to Manipulation: Part I-Theory,” J. Dyn. Syst. Meas. Control, vol. 107, no. 1, p. 1, 1985.
-
- Losey DP, Erwin A, McDonald CG, Sergi F, and O’Malley MK, “A Time-Domain Approach to Control of Series Elastic Actuators: Adaptive Torque and Passivity-Based Impedance Control,” IEEE/ASME Trans. Mechatronics, vol. 21, no. 4, pp. 2085–2096, 2016.
-
- Hollander KW et al., “An Efficient Robotic Tendon for Gait Assistance,” J. Biomech. Eng, vol. 128, no. 5, p. 788, 2006. - PubMed
-
- Bicchi A and Tonietti G, “Fast and “Soft-Arm” Tactics,” IEEE Robot. Autom. Mag, vol. 11, no. 2, pp. 22–33, 2004.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

