Dynamics from elastic neutron-scattering via direct measurement of the running time-integral of the van Hove distribution function

Abstract

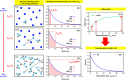
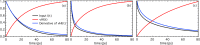
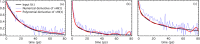
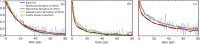
We present a new neutron-scattering approach to access the van Hove distribution function directly in the time domain, I(t), which reflects the system dynamics. Currently, I(t) is essentially determined from neutron energy-exchange. Our method consists of the straightforward measurement of the running time-integral of I(t), by computing the portion of scattered neutrons corresponding to species at rest within a time t, (conceptually elastic scattering). Previous attempts failed to recognise this connection. Starting from a theoretical standpoint, a practical realisation is assessed via numerical methods and an instrument simulation.

Figure 1

Illustration of the concept. Column 1 sketches the energy landscape of a system of particles, at three different observation times, t_obs. t_obs is the time-resolution of the measurement and is inversely proportional to the instrumental energy-resolution. At short t_obs only the rapid motions are detected, most of the system appearing at rest (1a). At intermediate t_obs other motions are detected (1b), and for long t_obs the slower motions are also detected (1c). Existing techniques require determination of many exchanged energy values, ΔE, to access I(t), typically operating at fixed t_obs. In general, our approach of obtaining the proportion of particles “at rest”, as a function of t_obs, should be more efficient. This proportion formally corresponds to the running time-integral of I(t) of Eq. 2, that is the van Hove integral vHI(t = t_obs), as sketched in column 2, in which each t_obs determines the upper integration limit of I(t). Differentiation of the measured vHI(t) (3a) provides I(t) directly (3b).

Figure 2

Numerical validations. The three plots are: (a) single exponential (with tau = 20 ps), (b) double exponential (with tau₁ = 20 ps, and tau₂ is twice as intense with = 2 ps), and (c) stretched exponential (with tau = 20 ps, and beta = 0.6). The other relevant parameters are: 20 < ħΔω_R < 15000 micro-eV corresponding to 0.127 < t_obs < 83 picoseconds; ħΔω_F = 10 micro-eV. There are no counting errors, which allows the consequences of using a Gaussian for R and F to be assessed.

Figure 3

Numerical validation with counting error (described in the text). The three plots are: (a) single exponential, (b) double exponential, and (c) stretched exponential. The numerical derivative of vHI(t) is intractable, but its polynomial derivative reproduces the input function well. Ranges are as in Fig. 2.

Figure 4

Numerical validation with counting error of several approaches to obtain I(t) from the “experimental” vHI(t). The three plots are: (a) single exponential, (b) double exponential, and (c) stretched exponential. The numerical derivative of vHI(t) is intractable, but its polynomial derivative and Gaussian-error derivative reproduce the input function well. The cosine FT is also shown for a consistency check. This figure is supposed for extending the results shown in Fig. 3 by showing that several approaches to get I(t) from vHI(t) are possible.

Figure 5

“Experimental” validation by a McStas simulation (of a new instrument designed to access vHI(t) directly). The 25 points (cyan) are the “measured” I(t) obtained by the numerical derivative of the “measured” vHI(t). Each of those 25 points has been measured (i) at 25 different monochromator-to-sample distances corresponding to 25 different value of Δω_R (so t_obs), (ii) but with fixed value of Δω_F, as per Eq. (1). The best fit of the “experimental” I(t)-points (red curve) agrees very well with the input I(t) (dashed black curve).