A framework for uncertainty and risk analysis in Total Maximum Daily Load applications
- PMID: 31396011
- PMCID: PMC6687321
- DOI: 10.1016/j.envsoft.2017.12.007
A framework for uncertainty and risk analysis in Total Maximum Daily Load applications
Abstract
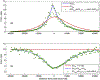
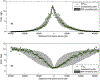
In the United States, the computation of Total Maximum Daily Loads (TMDL) must include a Margin of Safety (MOS) to account for different sources of uncertainty. In practice however, TMDL studies rarely include an explicit uncertainty analysis and the estimation of the MOS is often subjective and even arbitrary. Such approaches are difficult to replicate and preclude the comparison of results between studies. To overcome these limitations, a Bayesian framework to compute TMDLs and MOSs including an explicit evaluation of uncertainty and risk is proposed in this investigation. The proposed framework uses the concept of Predictive Uncertainty to calculate a TMDL from an equation of allowable risk of non-compliance of a target water quality standard. The framework is illustrated in a synthetic example and in a real TMDL study for nutrients in Sawgrass Lake, Florida.
Keywords: Bayesian analysis; Margin of safety; Risk assessment; Total Maximum Daily Load; Uncertainty analysis.
Figures
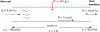


References
-
- Alameddine I, Cha Y, Reckhow KH, 2011. An evaluation of automated structure learning with Bayesian networks: an application to estuarine chlorophyll dynamics. Environ. Model. Software 26 (2), 163–172.
-
- Ambrose RB, Wool TA, Martin JL, 1993. The Water Quality Analysis Simulation Program, WASP5, Part a: Model Documentation. U.S. EPA Center for Exposure Assessment Modeling, Athens, GA.
-
- Ames DP, Lall U, 2008. Developing total maximum daily loads under uncertainty: decision analysis and the margin of safety. J. Contemp. Water Res. Educ. 140 (1), 37–52.
-
- Borsuk ME, Stow CA, Reckhow KH, 2002. Predicting the frequency of water quality standard Violations: a probabilistic approach for TMDL development. Environ. Sci. Technol. 36 (10), 2109–2115. - PubMed
-
- Camacho RA, Martin JL, McAnally W, Díaz-Ramirez J, Rodriguez H, Sucsy P, Zhang S, 2015. A comparison of bayesian methods for uncertainty analysis in hydraulic and hydrodynamic modeling. JAWRA J. Am. Water Res. Assoc. 51 (5), 1372–1393.
Grants and funding
LinkOut - more resources
Full Text Sources
