Active poroelastic two-phase model for the motion of physarum microplasmodia

Abstract

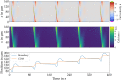
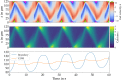
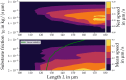
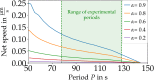
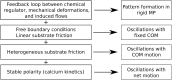
The onset of self-organized motion is studied in a poroelastic two-phase model with free boundaries for Physarum microplasmodia (MP). In the model, an active gel phase is assumed to be interpenetrated by a passive fluid phase on small length scales. A feedback loop between calcium kinetics, mechanical deformations, and induced fluid flow gives rise to pattern formation and the establishment of an axis of polarity. Altogether, we find that the calcium kinetics that breaks the conservation of the total calcium concentration in the model and a nonlinear friction between MP and substrate are both necessary ingredients to obtain an oscillatory movement with net motion of the MP. By numerical simulations in one spatial dimension, we find two different types of oscillations with net motion as well as modes with time-periodic or irregular switching of the axis of polarity. The more frequent type of net motion is characterized by mechano-chemical waves traveling from the front towards the rear. The second type is characterized by mechano-chemical waves that appear alternating from the front and the back. While both types exhibit oscillatory forward and backward movement with net motion in each cycle, the trajectory and gel flow pattern of the second type are also similar to recent experimental measurements of peristaltic MP motion. We found moving MPs in extended regions of experimentally accessible parameters, such as length, period and substrate friction strength. Simulations of the model show that the net speed increases with the length, provided that MPs are longer than a critical length of ≈ 120 μm. Both predictions are in line with recent experimental observations.

Fig 1. Sketch of the model.

Calcium regulates the gel’s active tension and varying calcium concentration levels cause gel deformations. When the gel moves, there is nonlinear friction between gel and substrate. Moreover, pressure gradients arise and there is friction between both phases. Both cause the fluid to start flowing and advecting the dissolved chemical species.

Fig 2. COM (orange) and boundary (blue) trajectories (top row) and calcium dynamics (bottom row) for regular (left column) and irregular (right column) motion with nonlinear substrate friction without calcium kinetics (ψ = 0).

The nonlinear substrate friction creates a spatially heterogeneous friction which allows for COM motion (orange line) together with motion of the boundaries (blue). The regular calcium dynamics (bottom left) results in oscillatory back and forth motion of COM as well as the boundaries (top left). An irregular calcium dynamics (bottom right) creates irregular motion (top right). There is no net motion for both cases. S1 and S2 Figs display a visual comparison of the calcium concentration plotted in the body reference and the laboratory frame. Parameters: v_slip = 6.0 μm/s α = 0.25, γ₀ = 10⁻⁵ kg/s, L = 130 μm, Pe = 50 (left) and v_slip = 30.0 μm/s, α = 0.3, γ₀ = 10⁻⁵ kg/s, Pe = 9.5, β = 10⁻⁴ kg μm⁻³ s⁻¹, E = 0.01 kg μm⁻¹ s⁻², η_g = 0.01 kg μm⁻¹ s⁻¹, η_f = 2 × 10⁻⁸ kg μm⁻¹ s⁻¹ (right).

Fig 3. Gel velocity (top), calcium dynamics (middle) and trajectories (bottom) of boundary (blue) and COM (orange) for type 1 motion.

Backward traveling calcium waves emerge periodically at the front, together with backward motion of the boundaries. Once the calcium wave is traveling backward, it causes forward gel flow and COM motion. On their arrival at the rear, the calcium concentration peaks, but the wave is annihilated upon collision with the boundary. The resulting forward gel motion is of a greater amplitude than the backward motion resulting in net motion with v_net = 0.2 μm/s. S3 Fig displays a visual comparison of the calcium concentration plotted in the body reference and the laboratory frame. Parameters B = 3.5, γ₀ = 7 × 10⁻⁶ kg/s, v_slip = 2.5 μm/s, α = 0.15, L = 160 μm and F = 12.3.

Fig 4. Gel velocity (left), calcium dynamics (middle) and trajectories (bottom) of boundary (blue) and COM (orange) for type 2 motion.

Calcium waves emerge alternating from front and back traveling towards the opposite side. The collision with a boundary sparks a new wave traveling backwards. Waves emerging at the front have a larger amplitude than waves originating at the rear resulting in net motion. S4 Fig displays a visual comparison of the calcium concentration plotted in the body reference and the laboratory frame. Parameters: B = 2, γ₀ = 10⁻⁵ kg/s, v_slip = 1.54 μm/s, α = 0.1, L = 125 μm and F = 18.5.

Fig 5. Net (top) and mean speed (bottom) for different strengths of base substrate friction γ₀ and length L.

Larger MPs possess both a higher net and mean speed. The net speed reaches a maximum for a medium base friction coefficient of γ₀ = 6 × 10⁻⁶ kg/s while the mean speed increases with decreasing friction. There is a critical length of L_cr ≈ 120 μm in the model and L needs to be larger than L_cr to transition from global calcium oscillations to states with motion of the boundaries. This is in qualitative agreement with the linear stability analysis that predicts the transition to an oscillatory short-wavelength instability (green line, bottom) at 130 μm for γ₀ = 6 × 10⁻⁶ kg/s. Parameters: B = 3.5, v_slip = 2.5 μm/s, α = 0.15 and F = 12.3.

Fig 6. A higher period P of the internal dynamics results in lower net speeds for type 1 motion.

For a period of more than P > 145 s there is a transition to global calcium oscillations without any motion. The experimentally observed periods are between 78 s and 127 s, taken from [13]. Parameters: B = 3.5, v_slip = 3.0 μm/s and F = 12.3.

Fig 7. Overview of the different levels in the model and corresponding types of locomotion.