Transient crosslinking kinetics optimize gene cluster interactions

Abstract

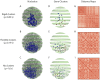
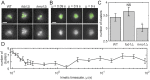
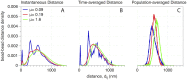
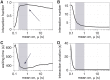
Our understanding of how chromosomes structurally organize and dynamically interact has been revolutionized through the lens of long-chain polymer physics. Major protein contributors to chromosome structure and dynamics are condensin and cohesin that stochastically generate loops within and between chains, and entrap proximal strands of sister chromatids. In this paper, we explore the ability of transient, protein-mediated, gene-gene crosslinks to induce clusters of genes, thereby dynamic architecture, within the highly repeated ribosomal DNA that comprises the nucleolus of budding yeast. We implement three approaches: live cell microscopy; computational modeling of the full genome during G1 in budding yeast, exploring four decades of timescales for transient crosslinks between 5kbp domains (genes) in the nucleolus on Chromosome XII; and, temporal network models with automated community (cluster) detection algorithms applied to the full range of 4D modeling datasets. The data analysis tools detect and track gene clusters, their size, number, persistence time, and their plasticity (deformation). Of biological significance, our analysis reveals an optimal mean crosslink lifetime that promotes pairwise and cluster gene interactions through "flexible" clustering. In this state, large gene clusters self-assemble yet frequently interact (merge and separate), marked by gene exchanges between clusters, which in turn maximizes global gene interactions in the nucleolus. This regime stands between two limiting cases each with far less global gene interactions: with shorter crosslink lifetimes, "rigid" clustering emerges with clusters that interact infrequently; with longer crosslink lifetimes, there is a dissolution of clusters. These observations are compared with imaging experiments on a normal yeast strain and two condensin-modified mutant cell strains. We apply the same image analysis pipeline to the experimental and simulated datasets, providing support for the modeling predictions.

Fig 1. Interphase yeast genome (A-C: Full, D-I: Nucleolus) using the polymer bead-spring model of [21] (see Section: Model) that implements transient SMC-protein-mediated crosslinking of 5k bp domains within the nucleolus on Chromosome XII.

The top, middle, and bottom rows depict chromosome conformations for three values of the kinetic timescale parameter μ: (top, μ = 0.09) induces rigid clusters; (center, μ = 0.19) induces flexible clusters; (bottom, μ = 1.6) induces no clusters. We identify the timescales with the intra-nucleolar clustering behavior they induce. (A)–(C) 3D “snapshots” of all 16 yeast chromosomes during interphase. Blue beads and edges highlight the nucleolus. (D)–(F) Visualization of nucleolar beads (5kbp chromosome domains) that self-organize into clusters. The beads’ positions are identical to those in (A)–(C) and their colors indicate their cluster labels, identified using modularity optimization [38] as described in Methods Section: Cluster identification via network community detection. (G)–(I) Heatmaps of the pairwise distances between beads in the nucleolus from one snapshot of the 4D time series, which provide an analogue of Hi-C bead-bead proximity data (see Methods Section: Pairwise-distance maps for high-throughput chromosome conformation capture (Hi-C)). Note that it is difficult to predict the absence/presence of clusters from heat maps.

Fig 2. Experimental images of the nucleolus.

Algorithmic thresholding of CDC14-GFP reveals alterations in nucleolar area and variance of signal intensity. (A) Top row depicts images of maximum intensity projection of WT, fob1Δ, and hmo1Δ yeast cells containing CDC14-GFP to label the nucleolus. Scale bar is 1 μm. The middle row are images of the binary mask generated by thresholding the projections using Otsu’s method. The bottom row are images of the projections where the intensities of pixels below the threshold were set to zero. See Methods Section: Image acquisition and baseline processing for more detail. (B) Bar chart of the nucleolar signal calculated by the area of the binary mask. (C) Bar chart of the standard deviation of normalized nucleolar signal. In panels (B) and (C), the non-significant changes are labeled ‘NS’ (see text), the bars represent an average value across n cells, and error bars indicate standard error.

Fig 3. Simulated microscope images for polymer bead-spring model with transient crosslinking and varying kinetic timescale μ.

Varying μ alters the area and variance of the intensity for the nucleolar signal, which models the affect of the fob1Δ and hmo1Δ mutations. (A) Timelapse montage of simulated microscope images for μ ∈ {0.09, 0.9, 9} (seconds). Scale bar is μm. (B) Area of nucleolus signal (μm²) as a function of μ ∈ [10⁻¹, 10²]. Areas were calculated by measuring the area of the binary mask generated by applying Otsu’s threshold to each image. (C) Standard deviation of the (non-normalized) nucleolus signal versus μ. (D) Standard deviation of the normalized nucleolus signals versus μ; these we normalized identically to the normalization of the experimental microscope images. In panels (B)-(D), error bars indicate standard errors observed using 22 time points for each value of μ.

Fig 4. Comparison of experimental and simulated microscope images.

Varying μ in the polymer bead-spring model captures the effect on nucleolus clustering incurred by the crosslink-altering mutations. (A) Maximum intensity projections of CDC14-GFP in WT, fob1Δ, and hmo1Δ cells with identified clusters marked by green circles. The lower row depicts the same images as the top row, except the circles are removed. (Images are the same as Fig 2(A)). (B) Same information as panel (A), except the results depict simulated images based on 4D simulation data for three values of μ. Scale bars in (A) and (B) are 1 μm. (C) Bar chart showing the number of clusters for each strain. The bars and error bars indicate the average and standard error across n cells, where n = 84, 70, and 77 for WT, fob1Δ, and hmo1Δ, respectively. Significance was assessed via a Student’s two-tailed T-test: p = 0.3 for WT versus fob1Δ and p = 0.04 for WT versus hmo1Δ. (D) Average number of clusters for simulated images as a function of μ. The averages and standard errors (see error bars) were calculated using 22 time points for each μ.

Fig 5. (A) Instantaneous distances, (B) time-average distances, and (C) population-averaged distances.

In each panel, we show results for the three kinetic regimes illustrated in Fig 1: μ = 0.09, μ = 0.19, and μ = 1.6. As reported in [21], multimodal histograms are a “signal” for the presence of clusters. This signal is strongest for μ = 0.09, is nonexistent for μ = 1.6, and we observe a new regime for μ = 0.19 (flexible clustering or cluster plasticity), whereby ‘soft’ clusters form but deform over time through cluster interactions.

Fig 6. Mixing statistics for gene interactions: (A) mixing fraction; (B) mean interaction number; (C) mean waiting time; and (D) mean interaction duration, which we plot as versus μ.

The shaded regions indicate the regime of flexible clustering, μ ∈ (0.19, 1). The arrows in panels (A) and (C) highlight that the interaction fraction and mean waiting time are both optimized for this range of μ. In contrast, this regime is associated with sharp transitions for the mean interaction number and duration, which both monotonically decrease with μ.

Fig 7. Cross communication describes the dynamics of community memberships of beads through community-level mixing.

We study cross-communication for a large range of μ by plotting four summary statistics: (A) communicating fraction; (B) mean interaction number; (C) mean waiting time; and (D) mean interaction duration (see text). The shaded regions indicate the regime of flexible clustering, μ ∈ (0.19, 1), and the arrows in panels (A) and (C) highlight that the interaction fraction and mean waiting time are both optimized for this range of μ. These results are qualitatively identical to the results in Fig 6 for gene mixing, illustrating that cluster formation and the exchanges of beads between clusters determine the timescale of mixing.

Fig 8. The birth and death of gene clusters identified using modularity-based community detection in temporal networks [37].

Panels (A), (B) and (C) depict the lifetime (i.e., duration) of each gene cluster versus the average cluster size for μ = 0.09, 0.19, and 1.6, respectively. The points’ colors have been chosen to highlight the density of points (with red indicating where there are many points close to one another). (D)–(F): The persistence (i.e., temporal coherence) of clusters is indicated by the probability that a randomly selected bead remains in the same cluster in the next time window, again plotted versus the average number of beads in that cluster. Results reflect d* = 325, γ = 10, ω = 1.