Kinetic asymmetry allows macromolecular catalysts to drive an information ratchet

Abstract

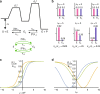
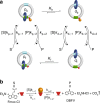
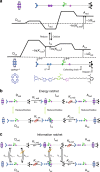
Molecular machines carry out their function by equilibrium mechanical motions in environments that are far from thermodynamic equilibrium. The mechanically equilibrated character of the trajectories of the macromolecule has allowed development of a powerful theoretical description, reminiscent of Onsager's trajectory thermodynamics, that is based on the principle of microscopic reversibility. Unlike the situation at thermodynamic equilibrium, kinetic parameters play a dominant role in determining steady-state concentrations away from thermodynamic equilibrium, and kinetic asymmetry provides a mechanism by which chemical free-energy released by catalysis can drive directed motion, molecular adaptation, and self-assembly. Several examples drawn from the recent literature, including a catenane-based chemically driven molecular rotor and a synthetic molecular assembler or pump, are discussed.

Fig. 1

Comparison between a macroscopic task and a microscopic information ratchet. Comparison of a moving a brick up a staircase in the macroscopic world, in which losses through friction are inevitable, and b an information ratchet appropriate for description of a molecular machine in the microscopic world where diffusion provides a mechanism for motion without loss owing to friction but in which the second law forbids net directed motion without the input of energy, and c how this can be described in terms of the four state mechanism for a minimal Brownian machine. Each clockwise cycle through the four states describes the movement of the “brick” one step to the right, where W = white, B = black, S = substrate, and P = product, and subscript L denotes the “bound” form of the motor as S and P lose their individual identity once bound to the motor, and $K_{\mathrm{b}}\mathrm{and}{K}_{\mathrm{f}}$ are equilibrium constants between the black and white stairs, respectively. Directionality of cycling in c is controlled by the position dependence of the rates for the binding/dissociation processes of S and P

Fig. 2

Kinetic asymmetry and Michaelis–Menten enzymes. a Energy profile for a Michaelis–Menten mechanism for catalysis, and two equivalent ways of writing the mechanism. An important quantity for determining the non-equilibrium behavior of the enzyme is the difference in transition state free-energies, $\Delta G^{‡}=G_1^{‡}-G_2^{‡}$, which can be expressed in terms of the rate constants as $\frac{k_{-1}}{k_{+2}}={\mathit{e}}^{-\Delta G^{‡}}$. This ratio does not depend on either μ or Δμ. b Bar graphs illustrating the equilibrium ($\Delta \mu =0$) distribution, where the kinetic asymmetry $k_{+2}∕k_{-1}$ has no role, and the non-equilibrium ($\Delta \mu =5$) steady-state distributions that strongly depend on the kinetic asymmetry $k_{+2}∕k_{-1}$. c, d The concentrations of substrate (S) and product (P) are taken as constant (i.e., chemo-stated) in all calculations, and can be written in terms of the chemical potential using activity coefficients $\left[\mathrm{S}\right]=a_{\mathrm{S}}{e}^{\mu +\Delta \mu }$ and $\left[\mathrm{P}\right]=a_{\mathrm{P}}{e}^{\mu -\Delta \mu }$. In ideal solutions both activity coefficients are ~ 1 in the units of concentration in which [S] and [P] are specified. Two types of enzyme adaptation: c “equilibrium” adaptation where the binding is based on the reference chemical potential $\mu -\Delta G^0,\Delta G^0=\left(G_{{\mathrm{E}}_{\mathrm{L}}}^0-G_{\mathrm{E}}^0\right)$, with $k_{-1}=5$, $k_{+2}=0.2$, and $\Delta \mu =3.4$ (orange); $\Delta \mu =0$ (green); and $\Delta \mu =-3.4$ (blue). d Non-equilibrium adaptation governed by Δμ plotted at fixed $\mu -\Delta G^0=0$. The binding is controlled by $\Delta \mu$ and by the kinetic asymmetry ($k_{+2}∕k_{-1}=25\left(\mathrm{blue}\right);k_{+2}∕k_{-1}=1\left(\mathrm{green}\right);\mathrm{and}{k}_{+2}∕k_{-1}=0.04\left(\mathrm{orange}\right)$)

Fig. 3

Four state synthetic rotor driven by a catalyzed reaction. a The rotor is based on that of Wilson et al. where a small benzylic amide macrocycle, shown as a dark blue ring, undergoes switching transitions between two different recognition sites, one shown as green and the other aqua. A catalytically active moiety near the green recognition site facilitates conversion of Fmoc-Cl to DBFV by a reaction shown in b. The symbol “p” indicates proximal, “d” indicates distal, “b” indicates that the catalytic site is bound, and “f” indicates that the catalytic site is free. The chemical potential difference driving conversion of Fmoc-Cl to DBFV under the experimental conditions of Wilson et al. is $\Delta \mu \approx 25$, slightly greater than the chemical potential difference driving ATP hydrolysis under physiological conditions, so the reaction is “far from equilibrium”. A key question is whether the blue ring undergoes clockwise or counter-clockwise rotation and what properties determine the direction of rotation?

Fig. 4

Kinetic lattice and energy landscape pictures showing how kinetic asymmetry leads to energy coupling. a A kinetic lattice model where the pathway favored by the kinetic asymmetry is shown in boldface. Having ${\mu }_{\mathrm{S}}>{\mu }_{\mathrm{P}}$ favors flux from top to bottom, and hence from right to left. b Contour plot of a 2-D energy landscape obtained by plotting the energies of the four states and six transition states and interpolating between the values

Fig. 5

Catalysis-driven information ratchet can undergo non-equilibrium adaptation. Kinetic mechanism for transitions between the states of the molecule, where the rate constants for the catalytic reactions are shown explicitly. The direct transition between states p_b and d_b is blocked—both forward and backward rate constants are very small—but the equilibrium constant must nonetheless reflect the relative energies of the two states

Fig. 6

An artificial molecular pump driven by external modulation or catalyzed redox reaction. a Schematic depiction of the pump with energy profiles under oxidizing and reducing conditions, along with molecular structures. b Energy ratchet model for operation of the pump by externally changing the redox potential back and forth between reducing and oxidizing conditions, and c Information ratchet model for using energy from a redox reaction ${\mathrm{red}}_1+{\mathrm{ox}}_2\begin{array}{c}\hfill \Delta \mu \hfill \\ \hfill \rightleftharpoons \hfill \\ \hfill \hfill \end{array}{\mathrm{red}}_2+{\mathrm{ox}}_1$ to drive assembly of CBPQT rings onto the collecting chain of the DB molecule, where disassembled (D), intermediate (I), and assembled (A) forms of the molecule when reduced (red) and when oxidized (ox) are shown

Fig. 7

Typical description of dissipative self-assembly in which inactive precursors are activated to a configuration that spontaneously undergoes self-assembly. a Model showing the kinetic cycle by which assembly can be controlled. Especially if dissociation of inactive monomers (defects) from the assembled structure is slow, maintaining S and P out of equilibrium will result in assembly. b Energy landscape model illustrating the “just-so” story in which input energy is used to promote the inactive monomers to an active form that undergoes spontaneous (exergonic) transition to the deactivated form. In fact, when the energy is provided by catalysis of a chemical reaction the free-energy for assembly of the active monomers on the blue surface is absolutely irrelevant