Phase-locking and bistability in neuronal networks with synaptic depression
- PMID: 31462839
- PMCID: PMC6713463
- DOI: 10.1016/j.physd.2017.09.007
Phase-locking and bistability in neuronal networks with synaptic depression
Abstract
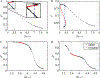
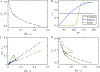
We consider a recurrent network of two oscillatory neurons that are coupled with inhibitory synapses. We use the phase response curves of the neurons and the properties of short-term synaptic depression to define Poincaré maps for the activity of the network. The fixed points of these maps correspond to phase-locked modes of the network. Using these maps, we analyze the conditions that allow short-term synaptic depression to lead to the existence of bistable phase-locked, periodic solutions. We show that bistability arises when either the phase response curve of the neuron or the short-term depression profile changes steeply enough. The results apply to any Type I oscillator and we illustrate our findings using the Quadratic Integrate-and-Fire and Morris-Lecar neuron models.
Keywords: Bistability; Coupled Oscillators; Phase Response Curve; Short-Term Synaptic Depression; Two-dimensional Poincarè Map.
Figures



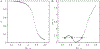




References
-
- Abbott L, Varela J, Sen K and Nelson S (1997) Synaptic depression and cortical gain control. Science 275:220–224. - PubMed
-
- Acker C, Kopell N, and White J (1999) Synchronization of strongly coupled excitatory neurons: relating network behavior to biophysics. Journal of Computational Neuroscience 15:71–90. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
