The effect of high-speed videoendoscopy configuration on reduced-order model parameter estimates by Bayesian inference

Abstract

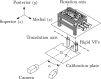
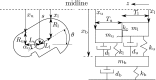
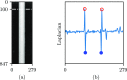
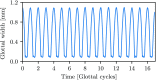
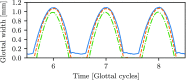
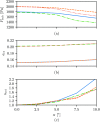
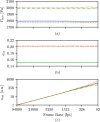
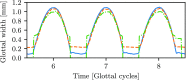
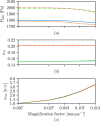
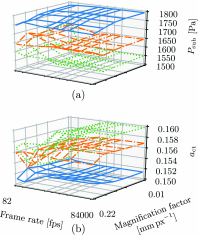
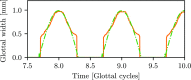
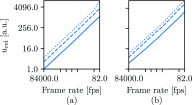
Bayesian inference has been previously demonstrated as a viable inverse analysis tool for estimating subject-specific reduced-order model parameters and uncertainties. However, previous studies have relied upon simulated glottal area waveforms with superimposed random noise as the measurement. In practice, high-speed videoendoscopy is used to measure glottal area, which introduces practical imaging effects not captured in simulated data, such as viewing angle, frame rate, and camera resolution. Herein, high-speed videos of the vocal folds were approximated by recording the trajectories of physical vocal fold models controlled by a symmetric body-cover model. Twenty videos were recorded, varying subglottal pressure, cricothyroid activation, and viewing angle, with frame rate and video resolution varied by digital video manipulation. Bayesian inference was used to estimate subglottal pressure and cricothyroid activation from glottal area waveforms extracted from the videos. The resulting estimates show off-axis viewing of 10° can lead to a 10% bias in the estimated subglottal pressure. A viewing model is introduced such that viewing angle can be included as an estimated parameter, which alleviates estimate bias. Frame rate and pixel resolution were found to primarily affect uncertainty of parameter estimates up to a limit where spatial and temporal resolutions were too poor to resolve the glottal area. Since many high-speed cameras have the ability to sacrifice spatial for temporal resolution, the findings herein suggest that Bayesian inference studies employing high-speed video should increase temporal resolutions at the expense of spatial resolution for reduced estimate uncertainties.

FIG. 1.

A schematic of the simulated HSV experimental setup. A pair of rigid two-dimensional VF medial surfaces (a coronal cross-section) are driven by a motion system that provides one translational and one rotational degree of freedom, as in the bar-plate VF model (Ref. 7). A consumer DSLR is used to capture the VF motion. A calibration plate with two dots, shown as circles, allow alignment of the camera view along a specified angle α.

FIG. 2.

The mapping procedure connects points on the BCM to points on the physical VF geometry. Each physical VF is controlled by two degrees of freedom (s and θ). These are mapped to the cover mass displacements (x_u and x_l) of the BCM. The rigid VF dimensions are given by: $L_{\mathrm{u}}=17.07\hspace{0.17em}\text{mm},\hspace{0.17em}{L}_{\mathrm{l}}=15.11\hspace{0.17em}\text{mm},\hspace{0.17em}{\alpha }_{\mathrm{u}}=27.71°,\hspace{0.17em}{R}_{\mathrm{l}}=22.23\hspace{0.17em}\text{mm}$, and $R_{\mathrm{u}}=14.29\hspace{0.17em}\text{mm}$.

FIG. 3.

(Color online) (a) Sample image extracted from a sample video recording. (b) The Laplacian computed using a 3 × 3 px kernel over row 100 of the image in (a). The open and closed circles are peaks of the Laplacian.

FIG. 4.

(Color online) The time averaged variance of the glottal width over rows of frames normalized by the variance at the highest resolution for various cases of known parameters and angles of view. Each point corresponds to the time averaged variance computed for one of the known $(P_{\text{sub}},a_{\text{ct}})$ cases at each of the angles of view $\alpha =(0°,2.5°,5.0°)$.

FIG. 5.

(Color online) Sample glottal width waveform extracted from HSV for $(P_{\text{sub}},a_{\text{ct}})=(1800\hspace{0.17em}\text{Pa},0.15)$ in physiological dimensions.

FIG. 6.

(Color online) Observed glottal width as a function of camera viewing angle α for (P_sub, a_ct) = (1800 Pa, 0.15). Angles of view correspond to: –––– $0°$, - - - $5°$, -·-· $10°$.

FIG. 7.

(Color online) The estimated (a) P_sub and (b) a_ct with increasing viewing angle. (c) The relative uncertainty with increasing viewing angle. Known reference parameters are: (P_sub, a_ct) = –––– (1800 Pa, 0.15), - - - (2000 Pa, 0.15), -·-· (1800 Pa, 0.20), …. (2000 Pa, 0.20).

FIG. 8.

(Color online) The estimated (a) P_sub and (b) a_ct with decreasing frame rate. (c) The relative uncertainty with decreasing frame rate. Known reference parameters are: $(P_{\text{sub}},a_{\text{ct}})=$ –––– (1800 Pa, 0.15), - - - (2000 Pa, 0.15), -·-· (1800 Pa, 0.20), …. (2000 Pa, 0.20).

FIG. 9.

(Color online) The measured glottal width waveform for various degrees of spatial downsampling. Each resolution corresponds to a magnification factor of approximately: –––– 0.013 mm px⁻¹, - - - 0.053 mm px⁻¹, -·-· 0.21 mm px⁻¹ for (P_sub, a_ct) = (1800 Pa, 0.15).

FIG. 10.

(Color online) The estimated (a) P_sub and (b) a_ct, and (c) relative uncertainty with decreasing spatial resolution. Known reference parameters are: (P_sub, a_ct) = ––––– (1800 Pa, 0.15), - - - (2000 Pa, 0.15), -·-· (1800 Pa, 0.20), …. (2000 Pa, 0.20). Note that the x axis corresponds to different downsampling factors of the spatial resolution.

FIG. 11.

(Color online) The estimated (a) P_sub and (b) a_ct. The known reference parameters are: $(P_{\text{sub}},a_{\text{ct}})=(1800\hspace{0.17em}\text{Pa},0.15)$ and viewing angles are: ––––– $0°$, -·-· $7.5°$, …. $10.0°$.

FIG. 12.

(Color online) The measured glottal widths at the highest —- and lowest -·-· resolutions at $\alpha =10°$ for (P_sub, a_ct) = (1800 Pa, 0.15).

FIG. 13.

(Color online) The relative uncertainty at (a) $\alpha =0°$ and (b) $\alpha =10°$ with changing spatial and temporal resolutions for the case $(P_{\text{sub}},a_{\text{ct}})=(1800\hspace{0.17em}\text{Pa},0.15)$. Different spatial resolutions correspond to: –––– ≈ 0.0066 [mm px⁻¹], -·-· ≈ 0.053 [mm px⁻¹] and …. ≈ 0.21 [mm px⁻¹].