Impact of Contact Constraints on the Dynamics of Idealized Intracranial Saccular Aneurysms

Abstract

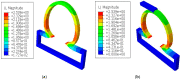
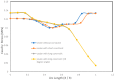
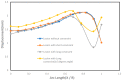
The rupture potential of intracranial aneurysms is an important medical question for physicians. While most intracranial (brain) aneurysms are asymptomatic, the quantification of rupture potential of both symptomatic and asymptomatic lesions is an active area of research. Furthermore, an intracranial aneurysm constrained by an optic nerve tissue might be a scenario for a physician to deal with during the treatment process. In this work, we developed a computational model of an idealized intracranial saccular aneurysm constrained by a rigid nerve tissue to investigate the impact of constrained nerve tissues on the dynamics of aneurysms. A comparative parametric study for constraints of varying length on aneurysm surface was considered. Our computational results demonstrated the impact of contact constraints on the level of stress near the fundus and provided insight on when these constraints can be protective and when they can be destructive. The results show that lesions with long contact constraints generated higher stress (0.116 MPa), whereas lesions without constraints generated less stress (0.1 MPa) at the fundus, which indicated that lesions with nerve constraints can be protective and less likely to rupture than the lesions without constraints. Moreover, lesions with point load on the fundus generated the highest stress (18.15 MPa) and, hence, they can be destructive.

Keywords: contact constraints; finite element analysis; intracranial aneurysms; nerve tissues; rupture potential.

Figure 1

(a) An idealized axisymmetric intracranial saccular aneurysm model; (b) long rigid contact constraint.

Figure 2

The computational geometric domain is partitioned into 6 subdomains to apply boundary conditions in each of the subdomains.

Figure 3

Finite element simulations of stresses (Pa) on axisymmetric intracranial saccular aneurysm for the cases where (a) lesions without constraints; (b) lesions with short contact constraints (20 mm); (c) lesions with long contact constraints (40 mm); (d) lesions with point load on the fundus; and (e) lesions with long contact constraints at an angle of 10 degrees from the horizontal axis. The associated stress results for all lesions were performed under the applied uniform pressure of P = 120 mmHg.

Figure 3

Finite element simulations of stresses (Pa) on axisymmetric intracranial saccular aneurysm for the cases where (a) lesions without constraints; (b) lesions with short contact constraints (20 mm); (c) lesions with long contact constraints (40 mm); (d) lesions with point load on the fundus; and (e) lesions with long contact constraints at an angle of 10 degrees from the horizontal axis. The associated stress results for all lesions were performed under the applied uniform pressure of P = 120 mmHg.

Figure 4

Finite element simulations of displacement (mm) on axisymmetric intracranial saccular aneurysm for the cases where (a) lesions without constraints; (b) lesions with short contact constraints (20 mm); (c) lesions with long contact constraints (40 mm); (d) lesions with point load on the fundus; and (e) lesions with long contact constraints at an angle of 10 degrees from the horizontal axis. The associated stress results for all lesions were performed under the applied uniform pressure of P = 120 mmHg.

Figure 4

Finite element simulations of displacement (mm) on axisymmetric intracranial saccular aneurysm for the cases where (a) lesions without constraints; (b) lesions with short contact constraints (20 mm); (c) lesions with long contact constraints (40 mm); (d) lesions with point load on the fundus; and (e) lesions with long contact constraints at an angle of 10 degrees from the horizontal axis. The associated stress results for all lesions were performed under the applied uniform pressure of P = 120 mmHg.

Figure 5

Effect of Cauchy stresses (MPa) with the undeformed arc length (X / R) on the axisymmetric intracranial saccular aneurysm for the cases where lesions without constraints, lesions with short constraints, lesions with long constraints, and lesions with long constraints at an angle of 10 degrees from the horizontal axis. Associated results were shown in both meridional and circumferential directions as a function of nondimensional undeformed arc length (X / R), where X = 0 corresponds to the fundus and X = R corresponds to the neck.

Figure 6

Effect of displacement (mm) with the undeformed arc length (X / R) on the axisymmetric intracranial saccular aneurysm for the cases where lesions without constraints, lesions with short constraints, lesions with long constraints, and lesions with long constraints at an angle of 10 degrees from the horizontal axis. Associated results were shown in both meridional and circumferential directions as a function of nondimensional undeformed arc length (X / R), where X = 0 corresponds to the fundus and X = R corresponds to the neck.