Delay in booster schedule as a control parameter in vaccination dynamics
- PMID: 31494722
- PMCID: PMC6858909
- DOI: 10.1007/s00285-019-01424-6
Delay in booster schedule as a control parameter in vaccination dynamics
Abstract
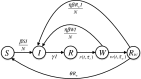
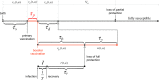
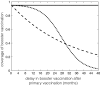
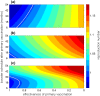
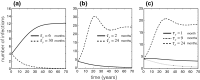
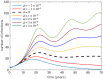
The use of multiple vaccine doses has proven to be essential in providing high levels of protection against a number of vaccine-preventable diseases at the individual level. However, the effectiveness of vaccination at the population level depends on several key factors, including the dose-dependent protection efficacy of vaccine, coverage of primary and booster doses, and in particular, the timing of a booster dose. For vaccines that provide transient protection, the optimal scheduling of a booster dose remains an important component of immunization programs and could significantly affect the long-term disease dynamics. In this study, we developed a vaccination model as a system of delay differential equations to investigate the effect of booster schedule using a control parameter represented by a fixed time-delay. By exploring the stability analysis of the model based on its reproduction number, we show the disease persistence in scenarios where the booster dose is sub-optimally scheduled. The findings indicate that, depending on the protection efficacy of primary vaccine series and the coverage of booster vaccination, the time-delay in a booster schedule can be a determining factor in disease persistence or elimination. We present model results with simulations for a vaccine-preventable bacterial disease, Heamophilus influenzae serotype b, using parameter estimates from the previous literature. Our study highlights the importance of timelines for multiple-dose vaccination in order to enhance the population-wide benefits of herd immunity.
Keywords: Booster schedule; Delay equations; Persistence; Reproduction number; Vaccination.
Figures
Similar articles
-
Modelling the effects of booster dose vaccination schedules and recommendations for public health immunization programs: the case of Haemophilus influenzae serotype b.BMC Public Health. 2017 Sep 13;17(1):705. doi: 10.1186/s12889-017-4714-9. BMC Public Health. 2017. PMID: 28903749 Free PMC article.
-
Vaccine failures after primary immunisation with Haemophilus influenzae type-b conjugate vaccine without booster.Lancet. 1997 Apr 26;349(9060):1197-202. doi: 10.1016/s0140-6736(96)06392-1. Lancet. 1997. PMID: 9130940
-
Effect of Haemophilus influenzae type b vaccination without a booster dose on invasive H influenzae type b disease, nasopharyngeal carriage, and population immunity in Kilifi, Kenya: a 15-year regional surveillance study.Lancet Glob Health. 2016 Mar;4(3):e185-94. doi: 10.1016/S2214-109X(15)00316-2. Epub 2016 Feb 5. Lancet Glob Health. 2016. PMID: 26853149 Free PMC article.
-
Spotlight on DTPa-HBV-IPV/Hib Vaccine (Infanrix hexa).BioDrugs. 2010 Oct 1;24(5):299-302. doi: 10.2165/11206690-000000000-00000. BioDrugs. 2010. PMID: 20795752 Review.
-
DTPa-HBV-IPV/Hib Vaccine (Infanrix hexa): A Review of its Use as Primary and Booster Vaccination.Drugs. 2010 May 28;70(8):1021-58. doi: 10.2165/11204830-000000000-00000. Drugs. 2010. PMID: 20481658 Review.
Cited by
-
Delays in the vaccination of infants between 2 and 18 months of age: associated factors in Chile.BMC Public Health. 2023 Sep 28;23(1):1882. doi: 10.1186/s12889-023-16769-3. BMC Public Health. 2023. PMID: 37770902 Free PMC article.
-
Short or Long Interval between Priming and Boosting: Does It Impact on the Vaccine Immunogenicity?Vaccines (Basel). 2021 Mar 20;9(3):289. doi: 10.3390/vaccines9030289. Vaccines (Basel). 2021. PMID: 33804604 Free PMC article.
-
Opinion Polls and Antibody Response Dynamics of Vaccination with COVID-19 Booster Vaccines.Vaccines (Basel). 2022 Apr 20;10(5):647. doi: 10.3390/vaccines10050647. Vaccines (Basel). 2022. PMID: 35632403 Free PMC article.
-
Safety and Immunogenicity of a Heterologous Booster of Protein Subunit Vaccine MVC-COV1901 after Two Doses of Adenoviral Vector Vaccine AZD1222.Vaccines (Basel). 2022 Oct 11;10(10):1701. doi: 10.3390/vaccines10101701. Vaccines (Basel). 2022. PMID: 36298566 Free PMC article.
-
Nonlinear model predictive control with logic constraints for COVID-19 management.Nonlinear Dyn. 2020;102(4):1965-1986. doi: 10.1007/s11071-020-05980-1. Epub 2020 Dec 2. Nonlinear Dyn. 2020. PMID: 33281298 Free PMC article.
References
-
- Briere EC, Rubin L, Moro PL, Cohn A, Clark T, Messonnier N, et al. Prevention and control of haemophilus influenzae type b disease: recommendations of the advisory committee on immunization practices (acip) MMWR Recomm Rep. 2014;63(RR–01):1–14. - PubMed
-
- Centers for Disease Control and Prevention et al (2009) Invasive haemophilus influenzae type b disease in five young children–Minnesota. Ann Emerg Med 54(1):83–85 - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical

