Consistent and correctable bias in metagenomic sequencing experiments
- PMID: 31502536
- PMCID: PMC6739870
- DOI: 10.7554/eLife.46923
Consistent and correctable bias in metagenomic sequencing experiments
Abstract
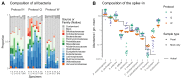
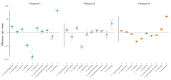
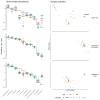
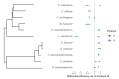
Marker-gene and metagenomic sequencing have profoundly expanded our ability to measure biological communities. But the measurements they provide differ from the truth, often dramatically, because these experiments are biased toward detecting some taxa over others. This experimental bias makes the taxon or gene abundances measured by different protocols quantitatively incomparable and can lead to spurious biological conclusions. We propose a mathematical model for how bias distorts community measurements based on the properties of real experiments. We validate this model with 16S rRNA gene and shotgun metagenomics data from defined bacterial communities. Our model better fits the experimental data despite being simpler than previous models. We illustrate how our model can be used to evaluate protocols, to understand the effect of bias on downstream statistical analyses, and to measure and correct bias given suitable calibration controls. These results illuminate new avenues toward truly quantitative and reproducible metagenomics measurements.
Keywords: 16S rRNA gene; bias; calibration; computational biology; infectious disease; metagenomics; microbiology; microbiome; reproducibility; systems biology.
© 2019, McLaren et al.
Conflict of interest statement
MM, AW, BC No competing interests declared
Figures

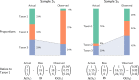
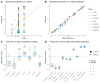
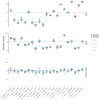

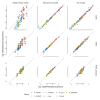



References
-
- Aitchison J. The Statistical Analysis of Compositional Data. London: Chapman and Hall; 1986.
-
- Aitchison J. On criteria for measures of compositional difference. Mathematical Geology. 1992;24:365–379. doi: 10.1007/BF00891269. - DOI
-
- Aitchison J. A concise guide to compositional data analysis. 2nd Compositional Data Analysis Workshop; 2003.
-
- Barceló-Vidal C, Martín-Fernández JA, Pawlowsky-Glahn V. Mathematical foundations of compositional data analysis. Proceedings of IAMG'01—The Sixth Annual Conference of the International Association for Mathematical Geology; 2001.
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

