Automated, unsupervised inversion of multiwavelength lidar data with TiARA: assessment of retrieval performance of microphysical parameters using simulated data
- PMID: 31503821
- PMCID: PMC7780543
- DOI: 10.1364/AO.58.004981
Automated, unsupervised inversion of multiwavelength lidar data with TiARA: assessment of retrieval performance of microphysical parameters using simulated data
Abstract
We evaluate the retrieval performance of the automated, unsupervised inversion algorithm, Tikhonov Advanced Regularization Algorithm (TiARA), which is used for the autonomous retrieval of microphysical parameters of anthropogenic and natural pollution particles. TiARA (version 1.0) has been developed in the past 10 years and builds on the legacy of a data-operator-controlled inversion algorithm used since 1998 for the analysis of data from multiwavelength Raman lidar. The development of TiARA has been driven by the need to analyze in (near) real time large volumes of data collected with NASA Langley Research Center's high-spectral-resolution lidar (HSRL-2). HSRL-2 was envisioned as part of the NASA Aerosols-Clouds-Ecosystems mission in response to the National Academy of Sciences (NAS) Decadal Study mission recommendations 2007. TiARA could thus also serve as an inversion algorithm in the context of a future space-borne lidar. We summarize key properties of TiARA on the basis of simulations with monomodal logarithmic-normal particle size distributions that cover particle radii from approximately 0.05 μm to 10 μm. The real and imaginary parts of the complex refractive index cover the range from non-absorbing to highly light-absorbing pollutants. Our simulations include up to 25% measurement uncertainty. The goal of our study is to provide guidance with respect to technical features of future space-borne lidars, if such lidars will be used for retrievals of microphysical data products, absorption coefficients, and single-scattering albedo. We investigate the impact of two different measurement-error models on the quality of the data products. We also obtain for the first time, to the best of our knowledge, a statistical view on systematic and statistical uncertainties, if a large volume of data is processed. Effective radius is retrieved to 50% accuracy for 58% of cases with an imaginary part up to 0.01i and up to 100% of cases with an imaginary part of 0.05i. Similarly, volume concentration, surface-area concentration, and number concentrations are retrieved to 50% accuracy in 56%-100% of cases, 99%-100% of cases, and 54%-87% of cases, respectively, depending on the imaginary part. The numbers represent measurement uncertainties of up to 15%. If we target 20% retrieval accuracy, the numbers of cases that fall within that threshold are 36%-76% for effective radius, 36%-73% for volume concentration, 98%-100% for surface-area concentration, and 37%-61% for number concentration. That range of numbers again represents a spread in results for different values of the imaginary part. At present, we obtain an accuracy of (on average) 0.1 for the real part. A case study from the ORCALES field campaign is used to illustrate data products obtained with TiARA.
Figures
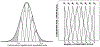



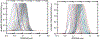
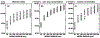









Similar articles
-
Arrange and average algorithm for the retrieval of aerosol parameters from multiwavelength high-spectral-resolution lidar/Raman lidar data.Appl Opt. 2014 Nov 1;53(31):7252-66. doi: 10.1364/AO.53.007252. Appl Opt. 2014. PMID: 25402885
-
Improved identification of the solution space of aerosol microphysical properties derived from the inversion of profiles of lidar optical data, part 2: simulations with synthetic optical data.Appl Opt. 2016 Dec 1;55(34):9850-9865. doi: 10.1364/AO.55.009850. Appl Opt. 2016. PMID: 27958481
-
Microphysical aerosol parameters from multiwavelength lidar.J Opt Soc Am A Opt Image Sci Vis. 2005 Mar;22(3):518-28. doi: 10.1364/josaa.22.000518. J Opt Soc Am A Opt Image Sci Vis. 2005. PMID: 15770990
-
Improved identification of the solution space of aerosol microphysical properties derived from the inversion of profiles of lidar optical data, part 3: case studies.Appl Opt. 2018 Apr 1;57(10):2499-2513. doi: 10.1364/AO.57.002499. Appl Opt. 2018. PMID: 29714234
-
Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols.Sensors (Basel). 2017 Jun 20;17(6):1450. doi: 10.3390/s17061450. Sensors (Basel). 2017. PMID: 28632170 Free PMC article. Review.
References
-
- Tikhonov AN and Arsenin VY, eds., Solutions of Ill-Posed Problems (Wiley, 1977).
-
- Müller D, “Inversionsalgorithmus zur bestimmung physikalischer partikeleigenschaften aus mehrwellenlängen-lidarmessungen (inversion algorithm for the determination of particle properties from multiwavelength lidar measurements),” Ph.D. thesis (Universität; 1997).
-
- Müller D, Wandinger U, Althausen D, Mattis I, and Ansmann A,”Retrieval of physical particle properties from lidar observations of extinction and backscatter at multiple wavelengths,” Appl. Opt 37, 2260–2263 (1998). - PubMed
-
- Müller D, Wandinger U, and Ansmann A, “Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: experiment,” Appl. Opt 39, 1879–1892 (2000). - PubMed
-
- Murayama T, Müller D, Wada K, Shimizu A, Sekigushi M, and Tsukamato T, “Characterization of Asian dust and Siberian smoke with multi-wavelength Raman lidar over Tokyo, Japan in spring 2003,” Geophys. Res. Lett 31, L23103 (2004).
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

