Organization of associating or crosslinked actin filaments in confinement
- PMID: 31525281
- PMCID: PMC6937401
- DOI: 10.1002/cm.21565
Organization of associating or crosslinked actin filaments in confinement
Abstract
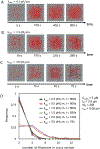
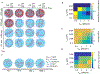
A key factor of actin cytoskeleton organization in cells is the interplay between the dynamical properties of actin filaments and cell geometry, which restricts, confines and directs their orientation. Crosslinking interactions among actin filaments, together with geometrical cues and regulatory proteins can give rise to contractile rings in dividing cells and actin rings in neurons. Motivated by recent in vitro experiments, in this work we performed computer simulations to study basic aspects of the interplay between confinement and attractive interactions between actin filaments. We used a spring-bead model and Brownian dynamics to simulate semiflexible actin filaments that polymerize in a confining sphere with a rate proportional to the monomer concentration. We model crosslinking, or attraction through the depletion interaction, implicitly as an attractive short-range potential between filament beads. In confining geometries smaller than the persistence length of actin filaments, we show rings can form by curving of filaments of length comparable to, or longer than the confinement diameter. Rings form for optimal ranges of attractive interactions that exist in between open bundles, irregular loops, aggregated, and unbundled morphologies. The probability of ring formation is promoted by attraction to the confining sphere boundary and decreases for large radii and initial monomer concentrations, in agreement with prior experimental data. The model reproduces ring formation along the flat plane of oblate ellipsoids.
Keywords: actin; computational modeling; confinement.
© 2019 Wiley Periodicals, Inc.
Figures
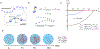





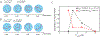


References
-
- Balasubramanian MK, Srinivasan R, Huang Y, and Ng K-H (2012). Comparing contractile apparatus-driven cytokinesis mechanisms across kingdoms. Cytoskeleton, 69(11):942–956. - PubMed
-
- Broedersz CP and MacKintosh FC (2014). Modeling semiflexible polymer networks. Reviews of Modern Physics, 86(3):995.
-
- Claessens MMAE, Bathe M, Frey E, and Bausch AR (2006a). Actin-binding proteins sensitively mediate f-actin bundle stiffness. Nat Mater, 5(9):748–753. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

