Realization of efficient quantum gates with a superconducting qubit-qutrit circuit

Abstract

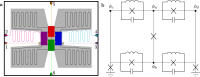
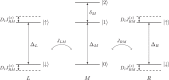
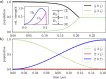
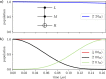
Building a quantum computer is a daunting challenge since it requires good control but also good isolation from the environment to minimize decoherence. It is therefore important to realize quantum gates efficiently, using as few operations as possible, to reduce the amount of required control and operation time and thus improve the quantum state coherence. Here we propose a superconducting circuit for implementing a tunable system consisting of a qutrit coupled to two qubits. This system can efficiently accomplish various quantum information tasks, including generation of entanglement of the two qubits and conditional three-qubit quantum gates, such as the Toffoli and Fredkin gates. Furthermore, the system realizes a conditional geometric gate which may be used for holonomic (non-adiabatic) quantum computing. The efficiency, robustness and universality of the presented circuit makes it a promising candidate to serve as a building block for larger networks capable of performing involved quantum computational tasks.

Figure 1

(a) Sketch of a possible physical implementation of the proposed circuit. Each colored box is a superconducting island corresponding to a node in a lumped circuit element model. Josephson junctions are shown schematically as yellow crosses. Bent black wires are inductors. The numbered colored lines are controls for readout and driving of the circuit: 1 and 3 are the flux lines for frequency tuning of the outer qubits, 2 and 4 are resonators capacitively coupled to left and right qubits, and lines 5 and 6 are control and driving of the two middle islands forming the middle qutrit. (b) Effective Lumped circuit scheme of the same circuit. The four nodes in the system are shown as dots and Josephson Junctions are shown as crosses.

Figure 2

Energy diagram of the system of two qubits (left, L, and right, R) and a qutrit (middle, M) described by the Hamiltonian in Equation (1). Also shown are the exchange couplings J_αM and state-dependent energy shifts $J_{\alpha M}^{(z)}$ of (1). D_i depend on the state of the qutrit $|i\rangle$, with, $D_0=0$, and typically, $D_1\gtrsim 2$ and $D_2\lesssim 4$.

Figure 3

(a) Populations of states $|0\rangle$, $|1\rangle$ and $|2\rangle$ of the middle qutrit during the half STIRAP in the case of off-resonant qutrit levels and $\max ({\mathrm{\Omega }}_{1,2})/2\pi =20\mathrm{MHz}$. The inset shows the envelopes of the mw pulses. (b) Dissociation of the initial state $|\downarrow 2\downarrow \rangle$ into the final state $|\uparrow 0\uparrow \rangle$ with the two-photon resonance ${\mathrm{\Delta }}_M+{\delta }_M={\mathrm{\Delta }}_L+{\mathrm{\Delta }}_R$ while the intermediate states $|\uparrow 1\downarrow \rangle$, $|\downarrow 1\uparrow \rangle$ are off-resonant. See Supplementary Note 2 for the parameters used in the simulation. We also include finite coherence times as described in Methods.

Figure 4

Numerical simulation of the implementation of the ccz gate in the rotating frame. The phase of the right qubit is flipped, $|0_H\rangle \to |1_H\rangle$, if the left qubit is in state $|\uparrow \rangle$ and the qutrit is in state $|0\rangle$, otherwise no change occurs as exemplified in (a) for the state $|\uparrow 20_H\rangle$ and in (b) for the state $|\downarrow 00_H\rangle$. A subsequent Hadamard gate on the right qubit will yield the desired ccnot gate. The standard circuit representation of the Toffoli gate is shown as an inset in the upper panel of the figure. See Supplementary Note 2 for the parameters used in the simulation.

Figure 5

(a and b) Numerical simulations of the acswap (almost cswap) gate for different computational basis states, with the exchange interaction $J_{\alpha M_{12}}$ resonant for time $T=\pi /\sqrt{2}{J}_{\alpha M_{12}}$. The standard circuit representation of the Fredkin gate is shown as an inset in the top part of the figure. (b) Numerical simulation of the full cswap gate for the initial superposition state $[\cos ({\theta }_1)|\uparrow \rangle +{\mathrm{e}}^{i{\phi }_1}\sin ({\theta }_1)|\downarrow \rangle ]$ $|1\rangle$ $[\cos ({\theta }_2)|\uparrow \rangle +{\mathrm{e}}^{i{\phi }_2}\sin ({\theta }_2)|\downarrow \rangle ]$ with ${\theta }_1=\pi /4$, ${\phi }_1=3\pi /4$, ${\theta }_2=3\pi /4$ and ${\phi }_2={\phi }_1$. In part 1, we perform the acswap operation during time $T_1=\pi /2J_{\alpha M_{01}}\simeq 0.025$ μs with the parameters as in panels (a and b). In part 2 we perform the ccz gate during time $T_2=2\pi /{\mathrm{\Omega }}_2$ with the resonant mw field of frequency ${\omega }_{\mathrm{mw}}={\delta }_M-2J_{\alpha M}^{(z)}$. The full cswap fidelity of this state is >0.98, with finite coherence times included. See Supplementary Note 2 for the parameters used in the simulation.

Figure 6

(a and b) Populations (left vertical axes) as function of time during the operation of the controlled-controlled holonomic gate in the case of $\theta =\pi /4$ and $\phi =0$. Panel (a) also shows the envelope of the external fields plotted with dotted lines with the corresponding vertical axis on the right of the plot. See Supplementary Note 2 for the parameters used in the simulation.

Figure 7

Populations of state versus θ ($\phi =0$) after the application of the controlled-controlled holonomic gate to the initial state $|\uparrow 0\uparrow \rangle$ (black and green points) and $|\downarrow 0\uparrow \rangle$ (red points). See Supplementary Note 2 for the parameters used in the simulation.