Default Priors for the Intercept Parameter in Logistic Regressions
- PMID: 31530966
- PMCID: PMC6748335
- DOI: 10.1016/j.csda.2018.10.014
Default Priors for the Intercept Parameter in Logistic Regressions
Abstract
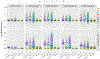
In logistic regression, separation occurs when a linear combination of predictors perfectly discriminates the binary outcome. Because finite-valued maximum likelihood parameter estimates do not exist under separation, Bayesian regressions with informative shrinkage of the regression coefficients offer a suitable alternative. Classical studies of separation imply that efficiency in estimating regression coefficients may also depend upon the choice of intercept prior, yet relatively little focus has been given on whether and how to shrink the intercept parameter. Alternative prior distributions for the intercept are proposed that downweight implausibly extreme regions of the parameter space, rendering regression estimates that are less sensitive to separation. Through simulation and the analysis of exemplar datasets, differences across priors stratified by established statistics measuring the degree of separation are quantified. Relative to diffuse priors, these proposed priors generally yield more efficient estimation of the regression coefficients themselves when the data are nearly separated. They are equally efficient in non-separated datasets, making them suitable for default use. Modest differences were observed with respect to out-of-sample discrimination. These numerical studies also highlight the interplay between priors for the intercept and the regression coefficients: findings are more sensitive to the choice of intercept prior when using a weakly informative prior on the regression coefficients than an informative shrinkage prior.
Keywords: Bayesian Methods; Exponential-Power Distribution; Pivotal Separation; Quasi-Complete Separation; Rare Events.
Figures
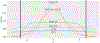
References
-
- Albert A, Anderson J. On the existence of maximum likelihood estimates in logistic regression models. Biometrika 1984;71(1):1–10.
-
- Bedrick E, Christensen R, Johnson W. A new perspective on priors for generalized linear models. Journal of the American Statistical Association 1996;91(436):1450–1460.
Grants and funding
LinkOut - more resources
Full Text Sources
