Boolean logic by convective obstacle flows

Abstract

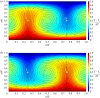
We present a potential new mode of natural computing in which simple, heat-driven fluid flows perform Boolean logic operations. The system comprises a two-dimensional single-phase fluid that is heated from below and cooled from above, with two obstacles placed on the horizontal mid-plane. The obstacles remove all vertical momentum that flows into them. The horizontal momentum extraction of the obstacles is controlled in a binary fashion, and constitutes the 2-bit input. The output of the system is a thresholded measure of the energy extracted by the obstacles. Due to the existence of multiple attractors in the phase space of this system, the input-output relationships are equivalent to those of the OR, XOR or NAND gates, depending on the threshold and obstacle separation. The ability to reproduce these logical operations suggests that convective flows might have the potential to perform more general computations, despite the fact that they do not involve electronics, chemistry or multiple fluid phases.

Keywords: Boolean logic; computation; convection.

Figure 1.

System schematic showing the boundary temperatures T_h and T_c that drive convective heat flow from the lower to the top boundary. The two obstacles are shown as white crosses (their actual size is only approximately 0.8% of the system height H). The colouring shows the dimensionless temperature with red corresponding to T_h and blue to T_c. (Online version in colour.)

Figure 2.

Typical flow structure of a convective 2-obstacle flow in which the obstacles are separated by Δ_o = H, with different inputs: (a) [m_u1 m_u2] = [0 0], (see animation of this simulation (https://www.youtube.com/watch?v=IKBfdaL9Zr8)), (b) [m_u1 m_u2] = [0 1], (see animation of this simulation (https://www.youtube.com/watch?v=6D2PtErYHHY)). Obstacles are shown as white crosses (actual size is only approx. 0.8% of the system height). Colour shows the normalized temperature of the fluid. (Online version in colour.)

Figure 3.

Typical flow structure of a convective 2-obstacle flow in which the obstacles are separated by Δ_o = H, with different inputs: (a) [m_u1 m_u2] = [1 0], see animation of this simulation (https://www.youtube.com/watch?v=vj_tqCfPK-8), (b) [m_u1 m_u2] = [1 1], see animation of this simulation (https://www.youtube.com/watch?v=IHZrO9r0ff4). Obstacles are shown as white crosses (actual size is only approx. 0.8% of the system height). Colour shows the normalized temperature of the fluid. (Online version in colour.)

Figure 4.

Typical flow structure of a convective 2-obstacle flow in which the obstacles are separated by Δ_o = H/2, with different inputs: (a) [m_u1 m_u2] = [0 0], (see animation of this simulation (https://www.youtube.com/watch?v=CVTo8zuPS_w)), (b) [m_u1 m_u2] = [0 1], (see animation of this simulation (https://www.youtube.com/watch?v=Jtyu8zI46Bs)). Obstacles are shown as white crosses (actual size is only approx. 0.8% of the system height). Colour shows the normalized temperature of the fluid. (Online version in colour.)

Figure 5.

Typical flow structure of a convective 2-obstacle flow in which the obstacles are separated by Δ_o = H/2, with different inputs: (a) [m_u1 m_u2] = [1 0], (see animation of this simulation (https://www.youtube.com/watch?v=cv1jQWLiEpg)), (b) [m_u1 m_u2] = [1 1], (see animation of this simulation (https://www.youtube.com/watch?v=eUq6LgCENyU)). Obstacles are shown as white crosses (actual size is only approx. 0.8% of the system height). Colour shows the normalized temperature of the fluid. (Online version in colour.)