Extending Tests of Hardy-Weinberg Equilibrium to Structured Populations

Abstract

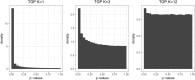
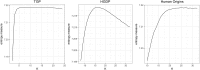
Testing for Hardy-Weinberg equilibrium (HWE) is an important component in almost all analyses of population genetic data. Genetic markers that violate HWE are often treated as special cases; for example, they may be flagged as possible genotyping errors, or they may be investigated more closely for evolutionary signatures of interest. The presence of population structure is one reason why genetic markers may fail a test of HWE. This is problematic because almost all natural populations studied in the modern setting show some degree of structure. Therefore, it is important to be able to detect deviations from HWE for reasons other than structure. To this end, we extend statistical tests of HWE to allow for population structure, which we call a test of "structural HWE." Additionally, our new test allows one to automatically choose tuning parameters and identify accurate models of structure. We demonstrate our approach on several important studies, provide theoretical justification for the test, and present empirical evidence for its utility. We anticipate the proposed test will be useful in a broad range of analyses of genome-wide population genetic data.

Keywords: Chi-square test; HWE; admixed; admixture; population genetics; quality control; random mating; significance test.

Figure 1

A proof of concept of the sHWE procedure. We fit the LFA model of structure (Hao et al. 2016) to the TGP data set and varied K, which is the number of latent factors to account for population structure. The left-most panel depicts a histogram of genome-wide P-values for a traditional test of HWE, which is equivalent to using the sHWE test with a population structure model of dimensionality $K=1$. The histogram is heavily skewed toward zero, showing that most SNPs would be identified as deviating from HWE. The middle panel depicts sHWE test P-values for $K=3$, which partially accounts for the population structure. As a result, there is less skew toward zero, and the large P-values (i.e., >0.75) are Uniform distributed which indicates that some SNPs are in sHWE. The right-most panel depicts sHWE test P-values for $K=12$, the empirically optimal value, which best accounts for population structure in the data set. The SNPs concentrated at the peak near zero are found to be deviated from sHWE, indicating that they violate HWE for reasons other than population structure.

Figure 2

The sHWE testing procedure as a schematic. Using the genotype matrix X, we first fit a model of population structure to estimate ${\widehat{\mathit{\pi }}}_{ij}.$ The values of ${\widehat{\mathit{\pi }}}_{ij}$ are used to simulate null data sets incorporating the sHWE assumptions. We compute sHWE test statistics for both observed and simulated null data sets and compute P-values by comparing the values of the observed test statistics and the pooled null test statistics.

Figure 3

Histogram of sHWE test P-values for each data set at chosen K as determined by the entropy measure. The sHWE test is performed for each SNP in the data set after fitting the LFA model of population structure. The aggregated P-values are mostly Uniform(0, 1) distributed, except for a peak at 0. This indicates that most of the SNPs are in sHWE, given the fitted structure. The peak at 0 contains an enrichment of SNPs that deviate from sHWE.

Figure 4

The entropy measure of uniformity of P-values for each data set as a function of K. For each model fit and value of K, the P-values for each data set were summarized by counting the number in each of 150 equal-sized bins in the range $\left[0,1\right].$ The bin closest to zero was dropped, as the most significant P-values will be in that bin. The proportion of counts in the 149 bins remaining are used to compute the entropy corresponding to K. Higher entropy means more Uniform.

Figure 5

Comparisons of significant sHWE P-values between the three data sets. For each pair of data sets, we choose the S most significant SNPs from one data set, where S is the greater of the number of significant SNPs at FDR q-value ≤ 20% for both data sets. We then test the corresponding S SNPs for sHWE in the other data set. Quantile–quantile plots of the resulting P-values vs. the Uniform(0, 1) quantiles shows that the deviations from sHWE are enriched in the other data set, verifying concordance of departures from sHWE between data sets.

Figure 6

Comparisons of sHWE P-values between TGP genotyping array data and the TGP variant calls. We identify significant SNPs at FDR q-value ≤ 20% for the two data sets, then plot quantile–quantile plots of the SNPs shared in the other data set against the Uniform distribution. The labelings follow the convention in Figure 5.