Time scales and wave formation in non-linear spatial public goods games
- PMID: 31545788
- PMCID: PMC6776369
- DOI: 10.1371/journal.pcbi.1007361
Time scales and wave formation in non-linear spatial public goods games
Abstract
The co-evolutionary dynamics of competing populations can be strongly affected by frequency-dependent selection and spatial population structure. As co-evolving populations grow into a spatial domain, their initial spatial arrangement and their growth rate differences are important factors that determine the long-term outcome. We here model producer and free-rider co-evolution in the context of a diffusive public good (PG) that is produced by the producers at a cost but evokes local concentration-dependent growth benefits to all. The benefit of the PG can be non-linearly dependent on public good concentration. We consider the spatial growth dynamics of producers and free-riders in one, two and three dimensions by modeling producer cell, free-rider cell and public good densities in space, driven by the processes of birth, death and diffusion (cell movement and public good distribution). Typically, one population goes extinct, but the time-scale of this process varies with initial conditions and the growth rate functions. We establish that spatial variation is transient regardless of dimensionality, and that structured initial conditions lead to increasing times to get close to an extinction state, called ε-extinction time. Further, we find that uncorrelated initial spatial structures do not influence this ε-extinction time in comparison to a corresponding well-mixed (non-spatial) system. In order to estimate the ε-extinction time of either free-riders or producers we derive a slow manifold solution. For invading populations, i.e. for populations that are initially highly segregated, we observe a traveling wave, whose speed can be calculated. Our results provide quantitative predictions for the transient spatial dynamics of cooperative traits under pressure of extinction.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
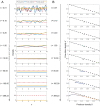

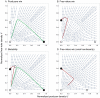
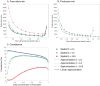
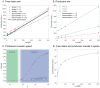
Similar articles
-
Persistence of cooperation in diffusive public goods games.Phys Rev E. 2019 Jun;99(6-1):062412. doi: 10.1103/PhysRevE.99.062412. Phys Rev E. 2019. PMID: 31330651
-
Evolution of cooperation in spatial public goods games with common resource dynamics.J Theor Biol. 2007 Aug 21;247(4):616-22. doi: 10.1016/j.jtbi.2007.04.008. Epub 2007 Apr 12. J Theor Biol. 2007. PMID: 17512952
-
Public goods games in populations with fluctuating size.Theor Popul Biol. 2018 May;121:72-84. doi: 10.1016/j.tpb.2018.01.004. Epub 2018 Feb 2. Theor Popul Biol. 2018. PMID: 29408219
-
Cooperation in Microbial Populations: Theory and Experimental Model Systems.J Mol Biol. 2019 Nov 22;431(23):4599-4644. doi: 10.1016/j.jmb.2019.09.023. Epub 2019 Oct 18. J Mol Biol. 2019. PMID: 31634468 Review.
-
Review: Game theory of public goods in one-shot social dilemmas without assortment.J Theor Biol. 2012 Apr 21;299:9-20. doi: 10.1016/j.jtbi.2011.06.018. Epub 2011 Jun 24. J Theor Biol. 2012. PMID: 21723299 Review.
Cited by
-
Spatial segregation and cooperation in radially expanding microbial colonies under antibiotic stress.ISME J. 2021 Oct;15(10):3019-3033. doi: 10.1038/s41396-021-00982-2. Epub 2021 May 5. ISME J. 2021. PMID: 33953363 Free PMC article.
-
Two-dimensional adaptive dynamics of evolutionary public goods games: finite-size effects on fixation probability and branching time.R Soc Open Sci. 2021 May 26;8(5):210182. doi: 10.1098/rsos.210182. R Soc Open Sci. 2021. PMID: 34084549 Free PMC article.
-
Spontaneous cell fusions as a mechanism of parasexual recombination in tumour cell populations.Nat Ecol Evol. 2021 Mar;5(3):379-391. doi: 10.1038/s41559-020-01367-y. Epub 2021 Jan 18. Nat Ecol Evol. 2021. PMID: 33462489
-
Integrating Mathematical Modeling with High-Throughput Imaging Explains How Polyploid Populations Behave in Nutrient-Sparse Environments.Cancer Res. 2020 Nov 15;80(22):5109-5120. doi: 10.1158/0008-5472.CAN-20-1231. Epub 2020 Sep 16. Cancer Res. 2020. PMID: 32938640 Free PMC article.
References
-
- Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. 10.1038/359826a0 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

