The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach

Abstract

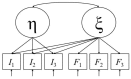
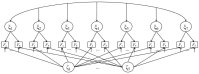
When a cognitive ability is assessed repeatedly, test scores and ability estimates are often observed to increase across test sessions. This phenomenon is known as the retest (or practice) effect. One explanation for retest effects is that situational test anxiety interferes with a testee's performance during earlier test sessions, thereby creating systematic measurement bias on the test items (interference hypothesis). Yet, the influence of anxiety diminishes with test repetitions. This explanation is controversial, since the presence of measurement bias during earlier measurement occasions cannot always be confirmed. It is argued that people from the lower end of the ability spectrum become aware of their deficits in test situations and therefore report higher anxiety (deficit hypothesis). In 2014, a structural equation model was proposed that specifically allows the comparison of these two hypotheses with regard to explanatory power for the negative anxiety-ability correlation found in cross-sectional assessments. We extended this model for usage in longitudinal studies to investigate the impact of test anxiety on test performance and on retest effects. A latent neighbor-change growth curve was implemented into the model that enables an estimation of retest effects between all pairs of successive test sessions. Systematic restrictions on model parameters allow testing the hypothetical reduction in anxiety interference over the test sessions, which can be compared to retest effect sizes. In an empirical study with seven measurement occasions, we found that a substantial reduction in interference upon the second test session was associated with the largest retest effect in a figural matrices test, which served as a proxy measure for general intelligence. However, smaller retest effects occurred up to the fourth test administration, whereas evidence for anxiety-induced measurement bias was only produced for the first two test sessions. Anxiety and ability were not negatively correlated at any time when the interference effects were controlled for. Implications, limitations, and suggestions for future research are discussed.

Keywords: cognitive abilities; figural matrices; intelligence; practice effect; retest effect; structural equation modeling; test anxiety.

Figure 1

Anxiety test (AT) model as proposed by Halpin et al. [36]. A latent cognitive ability variable (η) is measured by its respective manifest test items (three in this example: I₁, I₂, and I₃). A latent anxiety variable (ξ) is measured by its respective manifest questionnaire items (again, three in this example: F₁, F₂, and F₃). The arrows approaching the manifest variables from below represent their respective error terms. Regressions of the ability test items on latent anxiety are also modeled and reflect interference effects. The correlation between ability and anxiety is modeled and represents a potential deficit. Simultaneous modeling of interferences and deficits creates statistical rotational indeterminacy, rendering the model under-identified. However, strategic equality constraints among the factor loading parameters (for example: all interference effects are restricted to the same value) solve this problem.

Figure 2

Extension of the AT model [36] to longitudinal data (LAT model). An AT model (Figure 1) is constructed for every test session i (three in this example but it can be extended to any number of test sessions). States of latent cognitive ability (η_i) are modeled to correlate between test sessions. The same is applied to latent state anxiety (ξ_i).

Figure 3

Example of the full interference model with three test sessions. ξ_i (with i = 1, 2, 3) depicts situational test anxiety at measurement occasion i. We included a latent variable η^*₁ for a more comprehensible visualization of the model. η₁ regresses on η^*₁ with a regression weight of 1 and a residual-variance of 0. Hence, η^*₁ = η₁. Note that an inclusion of η^*₁ is not necessary for model estimation as η₁ can be used for the respective equations instead. By identifying the model by setting the variances of latent variables to 1, the latent differences variables δ_k,k−1 (with k = 2, 3) are on a standardized scale and their means can be interpreted as retest effect sizes in terms of Cohen’s d [80]. Interference effects in the third test session are depicted by dashed lines to illustrate the first step of the interference reduction approach. A model in which these coefficients are restricted to zero can be compared with the full interference model via a likelihood ratio test to test the null hypothesis that interferences disappear in the third test session.

Figure 4

Cognitive ability-confirmatory factor analysis (CFA). η₁–η₇ represent the latent ability variables measured by the figural matrices test items in every test session. I_1,1 represents the first item in the first test session, I_13,7 represents the 13th item of the seventh test session, etc. (items 2–12 of any test session are not shown but are represented by the respective three dots). Factor loadings can vary without any restrictions in a configural invariant model, but the loading of any item is restricted to the same respective value across test administrations when a more restrictive from of invariance is implemented. The threshold of any test item (not shown) is also restricted to the same respective value across test administrations when strong invariance is imposed. The arrows approaching the manifest variables from below represent their respective error-terms. The model was identified by setting the factor loading of the first item at every test session to 1.

Figure 5

Situational test anxiety-confirmatory factor analysis (STA-CFA). ξ₁–ξ₇ represent the latent STA variables measured by the fear-of-failure (FOF) items of the “Fragebogen zur Erfassung aktueller Motivation” (FAM) at every test session. F₁ represents the first item of the questionnaire and F₅ represents the fifth item. Items 2 to 4 are not shown, but are represented by the respective three dots. Loadings from latent STA variables on the manifest items can vary without any restrictions in a configural invariant model, but the loading of any item is restricted to the same respective value across test administrations when weak invariance is implemented. The free arrows approaching the manifest variables from below represent their respective error terms. Since the same items were applied in every test administration, five item-specific latent variables [93,94] were added to the model to account for indicator specific covariance. Only indicator-specific latent variables for items 1 and 5 are shown (ζ₁ and ζ_5, respectively), but the other three are represented by the three dots in between. The model was identified by setting the factor loading of the first item for every factor to 1.

Figure 6

Estimated means of the standardized latent difference variables of the full interference model, which can be interpreted as retest effect sizes in terms on Cohen’s d between two successive test administrations. To obtain these parameters, the model was identified by setting the variances of the latent variables to 1. d_2,1 represents the retest effect from the first to the second test administration, etc. Error-bars indicate two-tailed 95% confidence intervals. p-values at the top refer to the differences between the respective successive retest effects.