Massive computational acceleration by using neural networks to emulate mechanism-based biological models
- PMID: 31554788
- PMCID: PMC6761138
- DOI: 10.1038/s41467-019-12342-y
Massive computational acceleration by using neural networks to emulate mechanism-based biological models
Abstract
For many biological applications, exploration of the massive parametric space of a mechanism-based model can impose a prohibitive computational demand. To overcome this limitation, we present a framework to improve computational efficiency by orders of magnitude. The key concept is to train a neural network using a limited number of simulations generated by a mechanistic model. This number is small enough such that the simulations can be completed in a short time frame but large enough to enable reliable training. The trained neural network can then be used to explore a much larger parametric space. We demonstrate this notion by training neural networks to predict pattern formation and stochastic gene expression. We further demonstrate that using an ensemble of neural networks enables the self-contained evaluation of the quality of each prediction. Our work can be a platform for fast parametric space screening of biological models with user defined objectives.
Conflict of interest statement
The authors declare no competing interests.
Figures


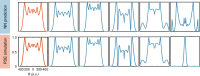

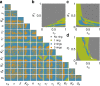
Similar articles
-
Mechanism-based organization of neural networks to emulate systems biology and pharmacology models.Sci Rep. 2024 May 27;14(1):12082. doi: 10.1038/s41598-024-59378-9. Sci Rep. 2024. PMID: 38802422 Free PMC article.
-
Efficient and scalable prediction of stochastic reaction-diffusion processes using graph neural networks.Math Biosci. 2024 Sep;375:109248. doi: 10.1016/j.mbs.2024.109248. Epub 2024 Jul 8. Math Biosci. 2024. PMID: 38986837
-
A new class of highly efficient exact stochastic simulation algorithms for chemical reaction networks.J Chem Phys. 2009 Jun 28;130(24):244104. doi: 10.1063/1.3154624. J Chem Phys. 2009. PMID: 19566139
-
Supervised learning in spiking neural networks: A review of algorithms and evaluations.Neural Netw. 2020 May;125:258-280. doi: 10.1016/j.neunet.2020.02.011. Epub 2020 Feb 25. Neural Netw. 2020. PMID: 32146356 Review.
-
A tutorial introduction to stochastic simulation algorithms for belief networks.Artif Intell Med. 1993 Aug;5(4):315-40. doi: 10.1016/0933-3657(93)90020-4. Artif Intell Med. 1993. PMID: 8220686 Review.
Cited by
-
A novel framework for the evaluation of coastal protection schemes through integration of numerical modelling and artificial intelligence into the Sand Engine App.Sci Rep. 2023 May 27;13(1):8610. doi: 10.1038/s41598-023-35801-5. Sci Rep. 2023. PMID: 37244960 Free PMC article.
-
AI-driven prediction of SARS-CoV-2 variant binding trends from atomistic simulations.Eur Phys J E Soft Matter. 2021 Oct 6;44(10):123. doi: 10.1140/epje/s10189-021-00119-5. Eur Phys J E Soft Matter. 2021. PMID: 34613523 Free PMC article.
-
Deep Neural Networks for Predicting Single-Cell Responses and Probability Landscapes.ACS Synth Biol. 2023 Aug 18;12(8):2367-2381. doi: 10.1021/acssynbio.3c00203. Epub 2023 Jul 19. ACS Synth Biol. 2023. PMID: 37467372 Free PMC article.
-
Systems Biology Approaches to Understanding COVID-19 Spread in the Population.Methods Mol Biol. 2024;2745:233-253. doi: 10.1007/978-1-0716-3577-3_15. Methods Mol Biol. 2024. PMID: 38060190
-
Predictive biology: modelling, understanding and harnessing microbial complexity.Nat Rev Microbiol. 2020 Sep;18(9):507-520. doi: 10.1038/s41579-020-0372-5. Epub 2020 May 29. Nat Rev Microbiol. 2020. PMID: 32472051 Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

