Versatile laser-free trapped-ion entangling gates
- PMID: 31555055
- PMCID: PMC6759860
- DOI: 10.1088/1367-2630/ab0be5
Versatile laser-free trapped-ion entangling gates
Abstract
We present a general theory for laser-free entangling gates with trapped-ion hyperfine qubits, using either static or oscillating magnetic-field gradients combined with a pair of uniform microwave fields symmetrically detuned about the qubit frequency. By transforming into a 'bichromatic' interaction picture, we show that either or geometric phase gates can be performed. The gate basis is determined by selecting the microwave detuning. The driving parameters can be tuned to provide intrinsic dynamical decoupling from qubit frequency fluctuations. The gates can be implemented in a novel manner which eases experimental constraints. We present numerical simulations of gate fidelities assuming realistic parameters.
Keywords: atomic physics; geometric phase gates; quantum computing; quantum gates; quantum logic; quantum physics; trapped-ions.
Figures
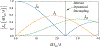

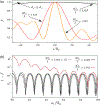
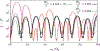
References
-
- Cirac JI and Zoller P 1995. Phys. Rev. Lett 74 4091. - PubMed
-
- Monroe C, Meekhof DM, King BE, Itano WM and Wineland DJ 1995. Phys. Rev. Lett 75 4714. - PubMed
-
- Nielsen MA and Chuang IL 2010. Quantum Computation and Quantum Information (Cambridge: Cambridge University Press; )
-
- Häffner H, Roos CF and Blatt R 2008. Phys. Rep 469 155
-
- Blatt R and Wineland DJ 2008. Nature 453 1008. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
