Structural puzzles in virology solved with an overarching icosahedral design principle

Abstract

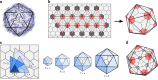
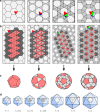
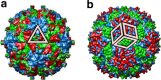
Viruses have evolved protein containers with a wide spectrum of icosahedral architectures to protect their genetic material. The geometric constraints defining these container designs, and their implications for viral evolution, are open problems in virology. The principle of quasi-equivalence is currently used to predict virus architecture, but improved imaging techniques have revealed increasing numbers of viral outliers. We show that this theory is a special case of an overarching design principle for icosahedral, as well as octahedral, architectures that can be formulated in terms of the Archimedean lattices and their duals. These surface structures encompass different blueprints for capsids with the same number of structural proteins, as well as for capsid architectures formed from a combination of minor and major capsid proteins, and are recurrent within viral lineages. They also apply to other icosahedral structures in nature, and offer alternative designs for man-made materials and nanocontainers in bionanotechnology.

Fig. 1

Capsid architecture according to Caspar and Klug theory. a Viruses exhibit the characteristic 5-, 3- and 2-fold rotational symmetry axes of icosahedral symmetry, indicated here with reference to the vertices, edges and faces of an icosahedral frame superimposed on the crystal structure of the $T=1$ STNV shell (figure based on PDB-ID 2BUK). b Construction of an icosahedral polyhedron via replacement of hexagons in a hexagonal lattice by the equivalent of 12 equidistant pentagons (red). Dark grey areas indicate parts of hexagons in the lattice that do not form part of the surface lattice of the final polyhedral shape. c One of the 20 triangles of the icosahedral frame is shown superimposed on the hexagonal grid for the four smallest polyhedra that can be constructed in CK theory. These are shown in increasingly lighter shades of blue: $T\left(1,0\right)=1$, $T\left(1,1\right)$ = 3, $T\left(2,0\right)=4$ and $T\left(2,1\right)=7$. The corresponding polyhedra (right) have 20 identical triangular faces corresponding to the triangles (left), one of which is shown in each case. d The CP positions are indicated with reference to the dual polyhedron, that is, the triangulated structure obtained by connecting midpoints of adjacent hexagons and pentagons in the surface lattice. CPs are positioned in the corners of the triangular faces (shown here as dots), and result in clusters (capsomers) of six (hexamers) and five (pentamers) CPs. The example shown corresponds to a $T=4$ layout, formed from 240 CPs that are organised as 12 pentamers (red) and 30 hexamers

Fig. 2

Design of icosahedral architectures from Archimedean lattices. a The four Archimedean lattices permitting the Caspar-Klug construction (from top to bottom): the hexagonal $\left(6,6,6\right)$, the trihexagonal $\left(3,6,3,6\right)$, the snub hexagonal $\left(3^4,6\right)$, and the rhombitrihexagonal $\left(3,4,6,4\right)$ lattice. In each case, the asymmetric unit (repeat unit of the lattice) is highlighted. Its overlap with the hexagonal sublattice used for the construction of the icosahedral polyhedra is shown in red. Apart from the case of the hexagonal lattice, this also includes a third of a triangular surface (blue), and in addition a triangle or a half square (both shown in green) for two of the lattices, respectively. b Construction of Archimedean solids via replacement of 12 hexagons by pentagons in analogy to the Caspar-Klug construction (see also Fig. 1b). c The polyhedral shapes corresponding to the examples shown in b. They each correspond to the smallest polyhedron in an infinite series of polyhedra for the given lattice type. Folded structures for larger elements in the new series are provided in Supplementary Fig. 2. d The smallest polyhedral shapes ($T_t$, $T_s$ and $T_r$, denoting polyhedra derived from the trihexagonal, snub hexagonal and rhombitrihexagonal lattices, respectively) are shown organised according to their sizes in context with the Caspar-Klug polyhedra. As surface areas scale according to Eq. (2) with respect to the Caspar-Klug geometries, the new solutions fall into the size gaps in between polyhedra in the Caspar-Klug series, or provide alternative layouts for capsids of the same size, as is the case for $T\left(2,0\right)=T_t\left(1,1\right)=4∕3T\left(1,1\right)=4$

Fig. 3

Viruses within a viral lineage adopting the same icosahedral series. Examples of viruses in the HK97 lineage, demonstrating that different members conform to the same family of icosahedral polyhedra: a Basilisk ($T_t\left(3,0\right)$), b HSV-1 ($T_t\left(4,0\right)$), c phage $\lambda$ ($T_t\left(2,1\right)$). The building blocks of their polyhedral surface lattices are shown in red (pentagons), blue (hexagons), and green (triangles) superimposed on figures adapted from (a), (b) and (c)

Fig. 4

Capsid protein interfaces are constrained by icosahedral geometry. The classification of icosahedral designs distinguishes between capsid layouts of viruses formed from the same number of proteins. Examples of a triangle and rhomb tiling are shown: a Pariacoto virus ($T^D\left(1,1\right)$); b MS2 ($T_t^D\left(1,1\right)$). Tiles are shown superimposed on figures adapted from the ViPER data base (Pariacoto virus: PDB-id 1f8v; MS2: PDB-id 2ms2)

Fig. 5

More general applications of the Archimedean lattice models in virology. a Rescaling of the triangular faces, with respect to the hexagonal ones, results in a gyrated version of the trihexagonal lattice in which proteins occupying different types of faces have identical footprints in the capsid surface. b The inner capsid of Pseudomonas phage phi6, a pseudo $T=2$ structure formed from 120 chains, is an example of a gyrated $T_t\left(1,0\right)$ lattice architecture. Its symmetry equivalent chains, shown in blue and green respectively based on RCSB PDB 4BTQ (ref. ), follow the layout of a surface architecture in which the surface areas of the triangular and pentagonal shapes occur in a ratio 3:5 (magenta), reflecting occupation by chains with comparable footprints on the capsid surface. c The kite tiling for Tobacco ringspot virus $\left(T_r^D\left(1,0\right)\right)$, with tiles shown superimposed on a figure adapted from the ViPER data base (Tobacco ringspot virus: PDB-id 1a6c). d A $T_t\left(2,1\right)$ lattice, shown superimposed on a surface representation in rainbow colouring of RCSB PDB 2XYY, captures the outermost features of bacteriophage P22, with timers indicating the positions of the crevasses between the radially most distal features of the capsomers. Triangles also mark the positions of the trimer interactions between capsomers at a lower radial level