Quantifying how diagnostic test accuracy depends on threshold in a meta-analysis

Abstract

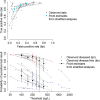
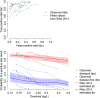
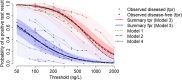
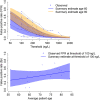
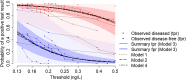
Tests for disease often produce a continuous measure, such as the concentration of some biomarker in a blood sample. In clinical practice, a threshold C is selected such that results, say, greater than C are declared positive and those less than C negative. Measures of test accuracy such as sensitivity and specificity depend crucially on C, and the optimal value of this threshold is usually a key question for clinical practice. Standard methods for meta-analysis of test accuracy (i) do not provide summary estimates of accuracy at each threshold, precluding selection of the optimal threshold, and furthermore, (ii) do not make use of all available data. We describe a multinomial meta-analysis model that can take any number of pairs of sensitivity and specificity from each study and explicitly quantifies how accuracy depends on C. Our model assumes that some prespecified or Box-Cox transformation of test results in the diseased and disease-free populations has a logistic distribution. The Box-Cox transformation parameter can be estimated from the data, allowing for a flexible range of underlying distributions. We parameterise in terms of the means and scale parameters of the two logistic distributions. In addition to credible intervals for the pooled sensitivity and specificity across all thresholds, we produce prediction intervals, allowing for between-study heterogeneity in all parameters. We demonstrate the model using two case study meta-analyses, examining the accuracy of tests for acute heart failure and preeclampsia. We show how the model can be extended to explore reasons for heterogeneity using study-level covariates.

Keywords: Box-Cox transformation; ROC curve; evidence synthesis; sensitivity; specificity; test cutoff.

Figure 1

Observed data on the accuracy of Brain Natriuretic Peptide (Triage assay only) in diagnosing acute heart failure across the full observed range of thresholds. Points from the same study are joined. tpr = true positive rate (sensitivity), fpr = false positive rate (1‐specificity). Also shown are point estimates with 95% credible intervals from a series of stratified bivariate meta‐analyses, in which similar thresholds are grouped and analysed together [Colour figure can be viewed at http://wileyonlinelibrary.com]

Figure 2

Observed data on the accuracy of spot urinary protein to creatinine ratio in detecting significant proteinuria in suspected preeclampsia. Points from the same study are joined. tpr = true positive rate (sensitivity), fpr = false positive rate (1‐specificity). Also shown are summary point estimates with 95% confidence intervals from an analysis by Riley et al15 [Colour figure can be viewed at http://wileyonlinelibrary.com]

Figure 3

Summary true positive rate (tpr) and false positive rate (fpr) estimates (Models 1‐4) for the Brain natriuretic peptide data across the full range of thresholds. 95% credible intervals and prediction intervals shown are from Model 3 [Colour figure can be viewed at http://wileyonlinelibrary.com]

Figure 4

Relationship between average patient age and false positive rate of Brain Natriuretic Peptide (Triage assay) in diagnosing acute heart failure (Model 5 results). Top panel: summary false positive rate across all thresholds for age 60 and age 80. Bottom panel: summary false positive rate at a threshold of 100 ng/litre, by average patient age. Shaded areas are 95% credible intervals [Colour figure can be viewed at http://wileyonlinelibrary.com]

Figure 5

Summary true positive rate (tpr) and false positive rate (fpr) estimates (Models 1‐4) for the protein to creatinine ratio data across the full range of thresholds. 95% credible intervals and prediction intervals shown are from Model 3 [Colour figure can be viewed at http://wileyonlinelibrary.com]